【题目】已知中心在坐标原点、焦点在x轴上的椭圆,它的离心率为![]() ,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
参考答案:
【答案】![]()
【解析】试题分析:设椭圆方程![]() (a>b>0),依题意椭圆方程可转化为
(a>b>0),依题意椭圆方程可转化为![]() ,与直线x+y﹣1=0联立,设M(x1,y1)、N(x2,y2),利用OM⊥ON可得x1x2+y1y2=0,利用韦达定理可得到关于b的关系式,从而可求得b2与a2.
,与直线x+y﹣1=0联立,设M(x1,y1)、N(x2,y2),利用OM⊥ON可得x1x2+y1y2=0,利用韦达定理可得到关于b的关系式,从而可求得b2与a2.
试题解析:
设椭圆方程为![]() +
+![]() =1(a>b>0),
=1(a>b>0),
∵e=![]() ,∴a2=4b2,即a=2b.
,∴a2=4b2,即a=2b.
∴椭圆方程为![]() +
+![]() =1.
=1.
把直线方程代入并化简,得5x2-8x+4-4b2=0.
设M(x1,y1)、N(x2,y2),则
x1+x2=![]() ,x1x2=
,x1x2=![]() (4-4b2).
(4-4b2).
∴y1y2=(1-x1)(1-x2)
=1-(x1+x2)+x1x2=![]() (1-4b2).
(1-4b2).
由于OM⊥ON,∴x1x2+y1y2=0.
解得b2=![]() ,a2=
,a2=![]() .
.
∴椭圆方程为![]() x2+
x2+![]() y2=1.
y2=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,F1,F2分别是椭圆C:
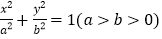 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.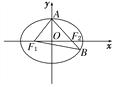
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40
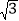 ,求a,b的值.
,求a,b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
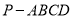 中,四边形
中,四边形 是直角梯形,
是直角梯形,  ,
,  ,
,  底面
底面 ,
,  ,
,  ,
,  是
是 的中点.
的中点.
(1)求证:平面
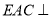 平面
平面 ;
;(2)若二面角
 的余弦值为
的余弦值为 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=4cosxsin(x+
 )﹣1.
)﹣1.
(1)求f(x)的最小正周期;
(2)若函数f(x)的定义域为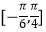 ,求单调递减区间和值域.
,求单调递减区间和值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1、OF2的中点分别为B1、B2,且△AB1B2是面积为4的直角三角形.
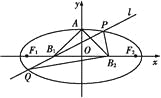
(1)求该椭圆的离心率和标准方程;
(2)过B1作直线交椭圆于P、Q两点,使PB2⊥QB2,求△PB2Q的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知sinα+cosα=
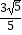 ,α∈(0,
,α∈(0,  ),sin(β﹣
),sin(β﹣  )=
)= 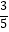 ,β∈(
,β∈(  ,
,  ).
).
(1)求sin2α和tan2α的值;
(2)求cos(α+2β)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
 )的部分图象如图所示.
)的部分图象如图所示. 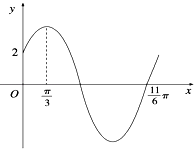
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移  个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
(3)当x∈[﹣ ,
, 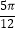 ]时,求函数y=f(x+
]时,求函数y=f(x+ 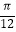 )﹣
)﹣ 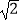 f(x+
f(x+  )的最值.
)的最值.
相关试题

