搜索
【题目】设两个非零向量 
和 
不共线．
（1）如果 
= + ， 
=2 +8 ， 
=3 ﹣3 ，求证：A、B、D三点共线；
（2）若| |=2，| |=3， 与 的夹角为60°，是否存在实数m，使得m + 与 ﹣ 垂直？并说明理由．
参考答案：
【答案】
（1）证明：∵ 
= 
+ 
+ 
=（ 
+ 
）+（ 
）+（ 
）
=6（ + ）=6
∴ 
且 与 有共同起点
∴A、B、D三点共线
（2）解：假设存在实数m，使得m 
与 
垂直，
则（m ）（ ）=0
∴ 
∵ 
=2， 
=3， 与 的夹角为60°
∴ 
， 
， 
∴4m+3（1﹣m）﹣9=0
∴m=6
故存在实数m=6，使得m 
与 垂直
【解析】（1）首先利用向量的加法运算，得到 ，然后观察与 的共线关系判断三点共线；（2）假设存在m，利用向量垂直，数量积为0，得到m的方程，解方程即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知sinx+cosx=1，则（sinx）2018+（cosx）2018= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各命题作为原命题，分别写出它们的逆命题、否命题和逆否命题．
(1)若α＝β，则sin α＝sin β；
(2)若对角线相等，则梯形为等腰梯形；
(3)已知a，b，c，d都是实数，若a＝b，c＝d，则a＋c＝b＋d.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，边长为2的正方形ABCD的顶点A，D，分别在x轴，y轴正半轴上移动，则
的最大值为 ．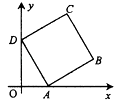 
-
科目： 来源： 题型：
查看答案和解析>>【题目】从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中，选出适当的一种填空：
(1)记集合A＝{－1，p,2}，B＝{2,3}，则“p＝3”是“A∩B＝B”的__________________；
(2)“a＝1”是“函数f(x)＝|2x－a|在区间
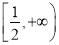上为增函数”的________________． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，F1，F2分别是椭圆C：
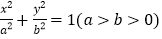的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，∠F1AF2＝60°.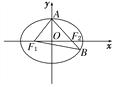
(1)求椭圆C的离心率；
(2)已知△AF1B的面积为40
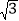，求a，b的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱锥
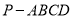中，四边形
是直角梯形， 
， 
， 
底面
， 
， 
， 
是
的中点．
（1）求证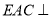：平面
平面
；（2）若二面角
的余弦值为
，求直线
与平面
所成角的正弦值．
相关试题
