【题目】已知函数f(x)=alnx,g(x)=x2 . 其中x∈R.
(1)若曲线y=f(x)与y=g(x)在x=1处的切线相互平行,求两平行直线间的距离;
(2)若f(x)≤g(x)﹣1对任意x>0恒成立,求实数a的值;
(3)当a<0时,对于函数h(x)=f(x)﹣g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为kAB , 若|kAB|≥1,求a的取值范围.
参考答案:
【答案】
(1)解: ![]() ,依题意得:a=2;
,依题意得:a=2;
∴曲线y=f(x)在x=1处的切线为2x﹣y﹣2=0,曲线y=g(x)在x=1处的切线方程为2x﹣y﹣1=0.
∴两直线间的距离为 ![]() =
= ![]()
(2)解:令h(x)=f(x)﹣g(x)+1,则 ![]()
当a≤0时,注意到x>0,∴h′(x)<0,∴h(x)在(0,+∞)单调递减,
又h(1)=0,故0<x<1时,h(x)>0,即f(x)>g(x)﹣1,与题设矛盾
当a>0时, ![]()
当 ![]() ,h′(x)>0,当
,h′(x)>0,当 ![]() 时,h′(x)<0
时,h′(x)<0
∴h(x)在(0, ![]() )上是增函数,在(
)上是增函数,在( ![]() ,+∞)上是减函数,
,+∞)上是减函数,
∴h(x)≤ ![]()
∵h(1)=0,又当a≠2时, ![]() 与
与 ![]() 不符.
不符.
∴a=2.
(3)解:当a<0时,由(2)知h′(x)<0,∴h(x)在(0,+∞)上是减函数,
不妨设0<x1≤x2,则|h(x1)﹣h(x2)|=h(x1)﹣h(x2),|x1﹣x2|=x2﹣x1,
∴|h(x1)﹣h(x2)|≥|x1﹣x2|等价于h(x1)﹣h(x2)≥x2﹣x1,即h(x1)+x1≥h(x2)+x2,
令H(x)=h(x)+x=alnx﹣x2+x+1,H(x)在(0,+∞)上是减函数,
∵ ![]() (x>0),
(x>0),
∴﹣2x2+x+a≤0在x>0时恒成立,
∴a≤(2x2﹣x)min
又x>0时,(2x2﹣x)min=﹣ ![]()
∴a≤﹣ ![]() ,
,
又a<0,∴a的取值范围是 ![]()
【解析】(1)求导函数,可得切线方程,利用平行线间的距离公式,可求两平行直线间的距离;(2)令h(x)=f(x)﹣g(x)+1,确定其单调性,分类讨论,即可求实数a的值;(Ⅲ)|h(x1)﹣h(x2)|≥|x1﹣x2|等价于h(x1)﹣h(x2)≥x2﹣x1 , 即h(x1)+x1≥h(x2)+x2 , 构造H(x)=h(x)+x=alnx﹣x2+x+1,H(x)在(0,+∞)上是减函数,可得﹣2x2+x+a≤0在x>0时恒成立,分离参数,即可求a的取值范围..
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点P是曲线
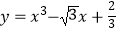 上的任意一点,点P处的切线的倾斜角为α,则α的取值范围为 .
上的任意一点,点P处的切线的倾斜角为α,则α的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
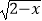 ﹣lg(x﹣1)的定义域是( )
﹣lg(x﹣1)的定义域是( )
A.[2,+∞)
B.(﹣∞,2)
C.(1,2]
D.(1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.y=1,y=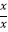
B.y=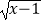 ×
× 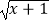 ,y=
,y= 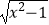
C.y=2x+1﹣2x , y=2x
D.y=2lgx,y=lgx2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0)的离心率为
(a>b>0)的离心率为  ,短轴长为
,短轴长为  ,过右焦点F的直线l与C相交于A,B两点.O为坐标原点.
,过右焦点F的直线l与C相交于A,B两点.O为坐标原点.
(1)求椭圆C的方程;
(2)若点P在椭圆C上,且 =
=  +
+  ,求直线l的方程.
,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=
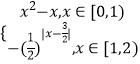 ,若x∈[﹣4,﹣2)时,f(x)≥
,若x∈[﹣4,﹣2)时,f(x)≥ 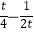 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
A.[﹣2,0)∪(0,1)
B.[﹣2,0)∪[1,+∞)
C.[﹣2,1]
D.(﹣∞,﹣2]∪(0,1] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)求平面ADC1与ABA1所成二面角的平面角的正弦值.
相关试题

