【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,短轴长为
,短轴长为 ![]() ,过右焦点F的直线l与C相交于A,B两点.O为坐标原点.
,过右焦点F的直线l与C相交于A,B两点.O为坐标原点.
(1)求椭圆C的方程;
(2)若点P在椭圆C上,且 ![]() =
= ![]() +
+ ![]() ,求直线l的方程.
,求直线l的方程.
参考答案:
【答案】
(1)解:由2b=2 ![]() .得b=
.得b= ![]() ,
,
即有 ![]() =
= ![]() ,a2﹣c2=2,
,a2﹣c2=2,
所以 ![]() ,
,
则椭圆方程为 ![]()
(2)解:椭圆C的方程为2x2+3y2=6.设A(x1,y1),B(x2,y2).
(ⅰ)当l不垂直于x轴时,设l的方程为y=k(x﹣1).
C上的点P使 ![]() =
= ![]() +
+ ![]() 成立的充要条件是P点坐标为(x1+x2,y1+y2),
成立的充要条件是P点坐标为(x1+x2,y1+y2),
且2(x1+x2)2+3(y1+y2)2=6,
整理得2x12+3y12+2x22+3y22+4x1x2+6y1y2=6,
又A、B在椭圆C上,即2x12+3y12=6,2x22+3y22=6,
故2x1x2+3y1y2+3=0.①
将y=k(x﹣1)代入2x2+3y2=6,并化简得
(2+3k2)x2﹣6k2x+3k2﹣6=0,
于是x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
y1y2=k2(x1﹣1)(x2﹣1)= ![]() .
.
代入①解得k2=2,
因此,当k=﹣ ![]() 时,l的方程为
时,l的方程为 ![]() x+y﹣
x+y﹣ ![]() =0;
=0;
当k= ![]() 时,l的方程为
时,l的方程为 ![]() x﹣y﹣
x﹣y﹣ ![]() =0.
=0.
(ⅱ)当l垂直于x轴时,由 ![]() +
+ ![]() =(2,0)知,
=(2,0)知,
C上不存在点P使 ![]() =
= ![]() +
+ ![]() 成立.
成立.
综上,l的方程为 ![]() x±y﹣
x±y﹣ ![]() =0
=0
【解析】(1)由题意可得b= ![]() ,运用离心率公式和a,b,c的关系,可得a,进而得到椭圆方程;(2)设A(x1 , y1),B(x2 , y2).(ⅰ)当l不垂直于x轴时,设l的方程为y=k(x﹣1),代入椭圆方程,运用韦达定理和向量的坐标表示,解方程可得k;(ⅱ)当l垂直于x轴时,由向量的加法运算,即可判断.
,运用离心率公式和a,b,c的关系,可得a,进而得到椭圆方程;(2)设A(x1 , y1),B(x2 , y2).(ⅰ)当l不垂直于x轴时,设l的方程为y=k(x﹣1),代入椭圆方程,运用韦达定理和向量的坐标表示,解方程可得k;(ⅱ)当l垂直于x轴时,由向量的加法运算,即可判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
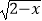 ﹣lg(x﹣1)的定义域是( )
﹣lg(x﹣1)的定义域是( )
A.[2,+∞)
B.(﹣∞,2)
C.(1,2]
D.(1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.y=1,y=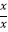
B.y=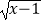 ×
× 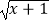 ,y=
,y= 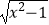
C.y=2x+1﹣2x , y=2x
D.y=2lgx,y=lgx2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=alnx,g(x)=x2 . 其中x∈R.
(1)若曲线y=f(x)与y=g(x)在x=1处的切线相互平行,求两平行直线间的距离;
(2)若f(x)≤g(x)﹣1对任意x>0恒成立,求实数a的值;
(3)当a<0时,对于函数h(x)=f(x)﹣g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为kAB , 若|kAB|≥1,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=
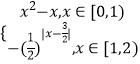 ,若x∈[﹣4,﹣2)时,f(x)≥
,若x∈[﹣4,﹣2)时,f(x)≥ 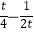 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
A.[﹣2,0)∪(0,1)
B.[﹣2,0)∪[1,+∞)
C.[﹣2,1]
D.(﹣∞,﹣2]∪(0,1] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)求平面ADC1与ABA1所成二面角的平面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为直角梯形,
为直角梯形,  ,
,  ,平面
,平面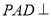 底面
底面 ,
,  为
为 的中点,
的中点,  是棱
是棱 上的点,
上的点,  ,
,  .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)若三棱锥
 的体积是四棱锥
的体积是四棱锥 体积的
体积的 ,设
,设 ,试确定
,试确定 的值.
的值.
相关试题

