【题目】直三棱柱![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,
,![]() 为棱
为棱![]() 上的点.
上的点.
(1)证明:![]() ;
;
(2)是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,说明点
?若存在,说明点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.

参考答案:
【答案】(1)略 (2)![]() 为
为![]() 的中点
的中点
【解析】试题分析:对于问题(1)可以先证明![]() 两两垂直,然后再建立空间直角坐标系用向量法进行证明;对于问题(2)可在(1)中建立的坐标系下,分别求出平面
两两垂直,然后再建立空间直角坐标系用向量法进行证明;对于问题(2)可在(1)中建立的坐标系下,分别求出平面![]() 与平面
与平面![]() 的法向量,再根据二面角的余弦公式,即可确定是否存在一点
的法向量,再根据二面角的余弦公式,即可确定是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.
试题解析:(1)证明:因为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() 面
面![]() ,
,
又因为![]() 面
面![]() ,
,
所以![]() ,
,
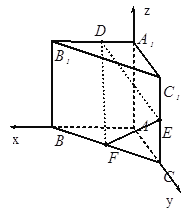
以![]() 为原点建立如图所示的空间直角坐标系
为原点建立如图所示的空间直角坐标系![]() ,则有
,则有
![]()
设![]() 且
且![]() ,即
,即![]() ,则
,则
![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]()
(2)结论:存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]()
理由如下:
由题可知面![]() 的法向量
的法向量![]()
设面![]() 的法向量为
的法向量为![]() ,则
,则
因为![]() ,
,
所以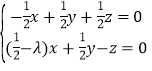 ,即
,即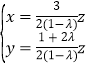 ,
,
令![]() ,则
,则![]()
因为平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ,
,
所以![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍),所以当
(舍),所以当![]() 为
为![]() 中点时满足要求
中点时满足要求
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,设倾斜角为
中,设倾斜角为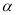 的直线
的直线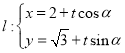 (
(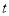 为参数)与曲线
为参数)与曲线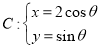 (
(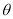 为参数)相交于不同的两点
为参数)相交于不同的两点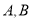 .
.(1)若
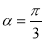 ,求线段
,求线段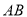 中点
中点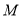 的坐标;
的坐标;(2)若
 ,其中
,其中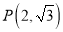 ,求直线
,求直线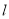 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
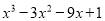 (x
(x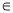 R),g(x)=2a-1
R),g(x)=2a-1(1)求函数f(x)的单调区间与极值.
(2)若f(x)≥g(x)对
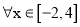 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(3,
 ),点B的极坐标为(6,
),点B的极坐标为(6,  ),曲线C:(x﹣1)2+y2=1
),曲线C:(x﹣1)2+y2=1
(1)求曲线C和直线AB的极坐标方程;
(2)过点O的射线l交曲线C于M点,交直线AB于N点,若|OM||ON|=2,求射线l所在直线的直角坐标方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,前n项和为Sn , 且Sn=
 ,数列{bn}的前n项和为Tn , 且bn=
,数列{bn}的前n项和为Tn , 且bn= 
(1)求数列{an}的通项公式;
(2)是否存在m,n∈N* , 使得Tn=am , 若存在,求出所有满足题意的m,n,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一动圆与圆
 外切,与圆
外切,与圆 内切.
内切.(1)求动圆圆心
 的轨迹
的轨迹 的方程.
的方程.(2)设过圆心
 的直线
的直线 与轨迹
与轨迹 相交于
相交于 两点,
两点, (
( 为圆
为圆 的圆心)的内切圆
的圆心)的内切圆 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某学校高三年级共
 名男生中随机抽取
名男生中随机抽取 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于 和
和 之间,将测量结果按如下方式分成八组,第一组
之间,将测量结果按如下方式分成八组,第一组 ;第二组
;第二组 ,
, ,第八组
,第八组 ,如图是按上述分组方法得到的频率分布直方图的一部分,若第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
,如图是按上述分组方法得到的频率分布直方图的一部分,若第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(
 )估计这所学校高三年级全体男生身高
)估计这所学校高三年级全体男生身高 以上(含
以上(含 )的人数.
)的人数.(
 )求第六组、第七组的频率并补充完整频率分布直方图.(铅笔作图并用中性笔描黑).
)求第六组、第七组的频率并补充完整频率分布直方图.(铅笔作图并用中性笔描黑).(
 )若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为
)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 、
、 ,求满足
,求满足 的事件概率.
的事件概率.
相关试题

