【题目】全网传播的融合指数是衡量电视媒体在中国网民中影响力的综合指标,根据相关报道提供的全网传播2017年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(1)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数;
(2)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 内的概率.
内的概率.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)用每组数据的中点值乘以该组的频率,再求和后可得所求的平均数.(2)列举出随机抽取2家的所有可能情况,根据古典概型概率公式求解.
详解:(1)这20家“省级卫视新闻台”的融合指数的平均数记为![]() ,
,
则![]() ,
,
即这20家“省级卫视新闻台”的融合指数的平均数为![]() .
.
(2)将融合指数在![]() 内的“省级卫视新闻台”记为
内的“省级卫视新闻台”记为![]() ;融合指数在
;融合指数在![]() 内的“省级卫视新闻台”记为
内的“省级卫视新闻台”记为![]() ,
,
由题得从中任意抽取2家的所有可能结果为![]()
![]()
![]() ,共10种.
,共10种.
记“至少有一家融合指数在![]() 内的省级卫视新闻台”为事件A,则事件A包含的情况有
内的省级卫视新闻台”为事件A,则事件A包含的情况有![]()
![]() ,共9种.
,共9种.
由古典概型概率公式可得![]() .
.
即至少有1家的融合指数在![]() 内的概率为
内的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知n为正整数,数列{an}满足an>0,4(n+1)an2﹣nan+12=0,设数列{bn}满足bn=

(1)求证:数列{ }为等比数列;
}为等比数列;
(2)若数列{bn}是等差数列,求实数t的值:
(3)若数列{bn}是等差数列,前n项和为Sn , 对任意的n∈N* , 均存在m∈N* , 使得8a12Sn﹣a14n2=16bm成立,求满足条件的所有整数a1的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
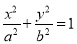 (
(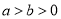 )的左右焦点分别为
)的左右焦点分别为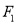 、
、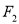 ,离心率
,离心率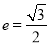 .过
.过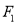 的直线交椭圆于
的直线交椭圆于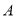 、
、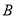 两点,三角形
两点,三角形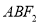 的周长为
的周长为 .
.(1)求椭圆的方程;
(2)若弦
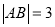 ,求直线
,求直线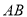 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,数列
,数列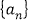 满足
满足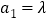 ,
,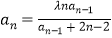
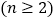 .
.(Ⅰ)当
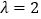 时,求证:数列
时,求证:数列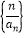 为等差数列并求
为等差数列并求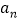 ;
;(Ⅱ)证明:对于一切正整数
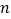 ,
,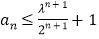 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
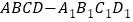 的棱长为
的棱长为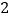 ,
,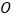 是
是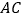 与
与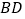 的交点,
的交点,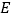 为
为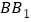 的中点.
的中点. (I)求证:直线
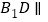 平面
平面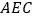 .
.(II)求证:
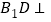 平面
平面 .
.(III)二面角
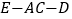 的余弦值.
的余弦值.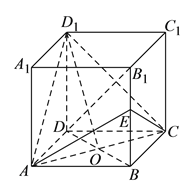
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过抛物线
 的焦点
的焦点 ,斜率为
,斜率为 的直线交抛物线于
的直线交抛物线于 两点,且
两点,且 .
.(1)求该抛物线
 的方程;
的方程;(2)已知抛物线上一点
 ,过点
,过点 作抛物线的两条弦
作抛物线的两条弦 和
和 ,且
,且 ,判断直线
,判断直线 是否过定点?并说明理由.
是否过定点?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个几何体的主视图与左视图是全等的长方形,边长分别是
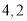 ,如图所示,俯视图是一个边长为
,如图所示,俯视图是一个边长为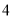 的正方形.
的正方形.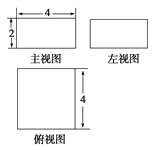
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
相关试题

