【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
参考答案:
【答案】(1)![]() ;(2)定点
;(2)定点![]()
【解析】试题分析:(1)利用点斜式设直线直线![]() 的方程,与抛物线联立方程组,结合韦达定理与弦长公式求
的方程,与抛物线联立方程组,结合韦达定理与弦长公式求![]() ,再根据
,再根据![]() 解得
解得![]() .(2)先设直线
.(2)先设直线![]() 方程
方程![]() , 与抛物线联立方程组,结合韦达定理化简
, 与抛物线联立方程组,结合韦达定理化简![]() ,得
,得![]() 或
或![]() ,代入
,代入![]() 方程可得直线
方程可得直线![]() 过定点
过定点![]()
试题解析:(1)拋物线的焦点![]() ,∴直线
,∴直线![]() 的方程为:
的方程为: ![]() .
.
联立方程组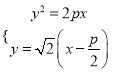 ,消元得:
,消元得: ![]() ,
,
∴![]() .
.
∴![]()
解得![]() .
.
∴抛物线![]() 的方程为:
的方程为: ![]() .
.
(2)由(1)可得点![]() ,可得直线
,可得直线![]() 的斜率不为0,
的斜率不为0,
设直线![]() 的方程为:
的方程为: ![]() ,
,
联立![]() ,得
,得![]() ,
,
则![]() ①.
①.
设![]() ,则
,则![]() .
.
∵![]()
![]()
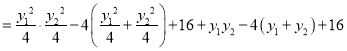
![]()
![]()
即![]() ,得:
,得: ![]() ,
,
∴![]() ,即
,即![]() 或
或![]() ,
,
代人①式检验均满足![]() ,
,
∴直线![]() 的方程为:
的方程为: ![]() 或
或![]() .
.
∴直线过定点![]() (定点
(定点![]() 不满足题意,故舍去).
不满足题意,故舍去).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定点
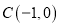 及椭圆
及椭圆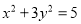 ,过点
,过点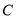 的动直线与椭圆相交于
的动直线与椭圆相交于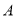 ,
, 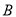 两点.
两点.(1)若线段
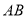 中点的横坐标是
中点的横坐标是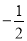 ,求直线
,求直线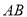 的方程;
的方程;(2)设点
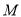 的坐标为
的坐标为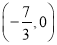 ,求证:
,求证: 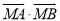 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)=
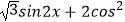 x+m在区间
x+m在区间 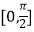 上的最小值为3,求常数m的值及此函数当x∈[a,a+π](其中a可取任意实数)时的最大值.
上的最小值为3,求常数m的值及此函数当x∈[a,a+π](其中a可取任意实数)时的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
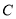 上的点到点
上的点到点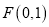 的距离比它到直线
的距离比它到直线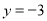 的距离小2.
的距离小2.(1)求曲线
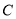 的方程;
的方程;(2)过点
 且斜率为
且斜率为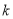 的直线
的直线 交曲线
交曲线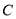 于
于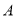 ,
, 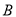 两点,若
两点,若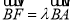 ,当
,当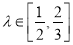 时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
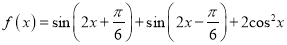 .
.(1)
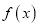 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(2)已知
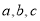 是
是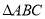 三边长,且
三边长,且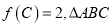 的面积
的面积 .求角
.求角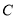 及
及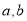 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4
 4:坐标系与参数方程
4:坐标系与参数方程在平面直角坐标系
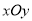 中,圆C的参数方程为
中,圆C的参数方程为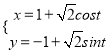 ,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线
,(t为参数),在以原点O为极点,x轴的非负半轴为极轴建立的极坐标系中,直线 的极坐标方程为
的极坐标方程为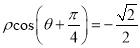 ,A,B两点的极坐标分别为
,A,B两点的极坐标分别为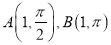 .
.(Ⅰ)求圆C的普通方程和直线
 的直角坐标方程;
的直角坐标方程;(Ⅱ)点P是圆C上任一点,求△PAB面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知1丈为10尺,该锲体的三视图如图所示,则该锲体的体积为( )
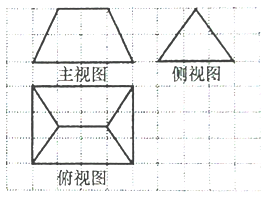
A. 10000立方尺 B. 11000立方尺 C. 12000立方尺 D. 13000立方尺
相关试题

