【题目】已知椭圆C: ![]() =1(a>b>0)的短轴长为2,离心率e=
=1(a>b>0)的短轴长为2,离心率e= ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+m与椭圆交于不同的两点A,B,与圆x2+y2= ![]() 相切于点M.
相切于点M.
(i)证明:OA⊥OB(O为坐标原点);
(ii)设λ= ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
参考答案:
【答案】解:(Ⅰ)∵2b=2,∴b=1.
又e= ![]() =
= ![]() ,a2=b2+c2 ,
,a2=b2+c2 ,
∴a2=2.
∴椭圆C的方程为 ![]() ;
;
(Ⅱ)(i)∵直线l:y=kx+m与圆x2+y2= ![]() 相切,
相切,
∴ ![]() ,即
,即 ![]() .
.
由  ,消去y并整理得,(1+2k2)x2+4kmx+2m2﹣2=0.
,消去y并整理得,(1+2k2)x2+4kmx+2m2﹣2=0.
设A(x1 , y1),B(x2 , y2),
则 ![]() .
.
∵ ![]() .
.
= ![]()
= ![]()
= ![]() ,
,
∴OA⊥OB.
(ii)∵直线l:y=kx+m与椭圆交于不同的两点A,B,
∴ ![]() ,
, ![]() .
.
∴  =
=  =
=  .
.
由(Ⅱ)(i)知x1x2+y1y2=0,
∴x1x2=﹣y1y2 ,  ,即
,即 ![]() .
.
∴  .
.
∵ ![]() ,
,
∴λ的取值范围是 ![]()
【解析】(Ⅰ)由已知得到b=1,结合e= ![]() ,即a2=b2+c2求得a2=2,则椭圆方程可求;(Ⅱ)(i)由直线l:y=kx+m与圆x2+y2=
,即a2=b2+c2求得a2=2,则椭圆方程可求;(Ⅱ)(i)由直线l:y=kx+m与圆x2+y2= ![]() 相切,可得
相切,可得 ![]() ,即
,即 ![]() .联立直线方程好椭圆方程,得到A,B横坐标的和与积,代入可得
.联立直线方程好椭圆方程,得到A,B横坐标的和与积,代入可得 ![]() ,得到OA⊥OB;(ii)直线l:y=kx+m与椭圆交于不同的两点A,B,把A,B的坐标代入椭圆方程,可得
,得到OA⊥OB;(ii)直线l:y=kx+m与椭圆交于不同的两点A,B,把A,B的坐标代入椭圆方程,可得 ![]() ,
, ![]() .在圆中由垂径定理可得
.在圆中由垂径定理可得 ![]() =
=  =
= ![]() .结合x1x2+y1y2=0,得到
.结合x1x2+y1y2=0,得到  .由x1 的范围求得λ的取值范围.
.由x1 的范围求得λ的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N* , 总有b1b2b3…bn﹣1bn=an+2成立.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=(﹣1)n ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列两个命题:
 函数
函数 在[2,+∞)单调递增;
在[2,+∞)单调递增;  关于
关于 的不等式
的不等式 的解集为
的解集为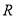 .若
.若 为真命题,
为真命题,  为假命题,求
为假命题,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看
不打算观看
女生
20
b
男生
c
25
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,右焦点为
,右焦点为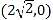 。斜率为1的直线
。斜率为1的直线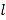 与椭圆
与椭圆 交于
交于 两点,以
两点,以 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为 。
。(1)求椭圆
 的方程;
的方程;(2)求
 的面积。
的面积。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=a(x﹣1)2+lnx+1,g(x)=f(x)﹣x,其中a∈R.
(Ⅰ)当a=﹣ 时,求函数f(x)的极值;
时,求函数f(x)的极值;
(Ⅱ)当a>0时,求函数g(x)的单调区间;
(Ⅲ)当x∈[1,+∞)时,若y=f(x)图象上的点都在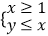 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图的程序框图,则输出S的值为( )

A.2016
B.2
C.
D.﹣1
相关试题

