【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年
的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年![]() 位居民毎人的月均用水量(单位:吨),将数据按照
位居民毎人的月均用水量(单位:吨),将数据按照![]() 分成
分成![]() 组,制成了如图所示的频率分布直方图.
组,制成了如图所示的频率分布直方图.
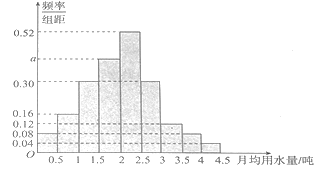
(1)求直方图中![]() 的值;
的值;
(2)若该市有![]() 万居民,估计全市居民中月均用水量不低于
万居民,估计全市居民中月均用水量不低于![]() 吨的人数,并说明理由;
吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到
的值(精确到![]() ),并说明理由.
),并说明理由.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 万;(3)2.73.
万;(3)2.73.
【解析】(1) 由概率统计相关知识,各组频率之和的值为![]() ,
,![]() 频率=(频率/组距)
频率=(频率/组距)![]() 组距,
组距,
![]() ,解得
,解得![]() .
.
(2) 由图,不低于![]() 吨的人数所占比例为
吨的人数所占比例为![]() ,
,![]() 全市月圴用水量不低于
全市月圴用水量不低于![]() 吨的人数为
吨的人数为![]() (万).
(万).
(3) 由图可知,月圴用水量小于![]() 吨的居民人数所占比例为
吨的居民人数所占比例为![]() .即
.即![]() 的居民用水量小于
的居民用水量小于![]() 吨,同理,
吨,同理,![]() 的居民用水量小于
的居民用水量小于![]() 吨,故
吨,故![]() .
.
假设月圴用水量平均分布,则![]() (吨).
(吨).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:以点
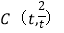 (
( )为圆心的圆与
)为圆心的圆与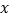 轴交
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线
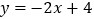 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五面体
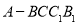 中,
中,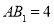 ,底面
,底面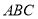 是正三角形,
是正三角形,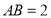 ,四边形
,四边形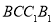 是矩形,二面角
是矩形,二面角 为直二面角.
为直二面角.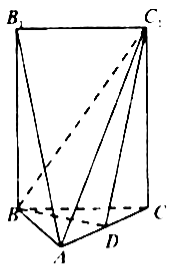
(1)
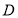 在
在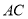 上运动,当
上运动,当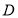 在何处时,有
在何处时,有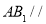 平面
平面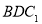 ,并说明理由;
,并说明理由;(2)当
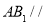 平面
平面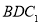 时,求二面角
时,求二面角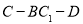 余弦值.
余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
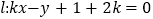 (
(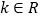 ).
).(1)证明:直线
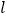 过定点;
过定点;(2)若直线不经过第四象限,求
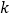 的取值范围;
的取值范围;(3)若直线
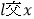 轴负半轴于
轴负半轴于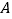 ,交
,交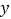 轴正半轴于
轴正半轴于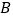 ,△
,△ 的面积为
的面积为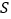 (
(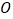 为坐标原点),求
为坐标原点),求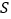 的最小值,并求此时直线
的最小值,并求此时直线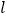 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:

(1) 算出线性回归方程
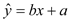 ; (a,b精确到十分位)
; (a,b精确到十分位)(2)气象部门预测下个月的平均气温约为3℃,据此估计,求该商场下个月毛衣的销售量.
(参考公式:
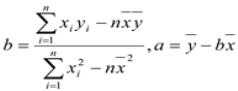 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—1:几何证明选讲
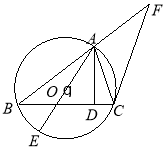
如图,已知圆
 是
是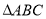 的外接圆,
的外接圆, 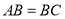 ,
,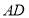 是
是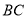 边上的高,
边上的高,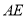 是圆
是圆 的直径,过点
的直径,过点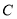 作圆
作圆 的切线交
的切线交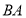 的延长线于点
的延长线于点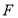 .
.
(Ⅰ)求证:
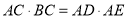 ;
; (Ⅱ)若
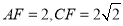 ,求
,求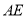 的长.
的长.
相关试题

