【题目】E为正四面体D﹣ABC棱AD的中点,平面α过点A,且α∥平面ECB,α∩平面ABC=m,α∩平面ACD=n,则m、n所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:如图,

由α∥平面ECB,且α∩平面ABC=m,α∩平面ACD=n,
结合面面平行的性质可得:m∥BC,n∥EC,
∴∠BCE为m、n所成角,
设正四面体的棱长为2,则BE=CE= ![]() ,
,
则cos∠BCE= ![]() .
.
故正确答案为:A.
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究某高校大学5000名新生的视力情况,随机地抽查了该校100名进校新生的视力情况,得到其频率分布直方图如右图,若规定视力低于5.0的学生属[于近视学生,则估计该校新生中不是近视的人数约为( )

A.300人
B.400人
C.600人
D.1000人 -
科目: 来源: 题型:
查看答案和解析>>【题目】某小朋友按如下规则练习数数,
 大拇指,
大拇指, 食指,
食指, 中指,
中指, 无名指,
无名指, 小指,
小指, 无名指,
无名指,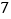 中指,
中指, 食指,
食指, 大拇指,
大拇指, 食指,
食指, ,一直数到
,一直数到 时,对应的指头是( )
时,对应的指头是( )
A. 小指 B. 中指 C. 食指 D. 无名指
-
科目: 来源: 题型:
查看答案和解析>>【题目】一批产品抽50件测试,其净重介于13克与19克之间,将测试结果按如下方式分成六组:第一组,净重大于等于13克且小于14克;第二组,净重大于等于14克且小于15克;…第六组,净重大于等于18克且小于19克.如图是按上述分组方法得到的频率分布直方图.设净重小于17克的产品数占抽取数的百分比为x,净重大于等于15克且小于17克的产品数为y,则从频率分布直方图中可分析出x和y分别为( )

A.0.9,35
B.0.9,45
C.0.1,35
D.0.1,45 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=loga(x+3)﹣1(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m,n均大于0,则
 的最小值为( )
的最小值为( )
A.2
B.4
C.8
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】在正四面体ABCD中,M,N分别是BC和DA的中点,则异面直线MN和CD所成角为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
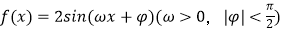 的两条相邻对称轴间的距离为
的两条相邻对称轴间的距离为  ,把f(x)的图象向右平移
,把f(x)的图象向右平移  个单位得到函数g(x)的图象,且g(x)为偶函数,则f(x)的单调递增区间为( )
个单位得到函数g(x)的图象,且g(x)为偶函数,则f(x)的单调递增区间为( )
A.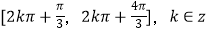
B.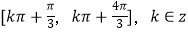
C.
D.
相关试题

