【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(I)若曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,求
轴,求![]() 的值;
的值;
(II)求函数![]() 的极值;
的极值;
(III)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() (2)当
(2)当![]() 时,函数
时,函数![]() 无极小值;当
无极小值;当![]() ,
, ![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.(3)1
,无极大值.(3)1
【解析】试题分析:(1)求出![]() ,由导数的几何意义,解方程
,由导数的几何意义,解方程![]() 即可;(2)解方程
即可;(2)解方程![]() ,注意分类讨论,以确定
,注意分类讨论,以确定![]() 的符号,从而确定
的符号,从而确定![]() 的单调性,得极大值或极小值(极值点多时,最好列表表示);(3)题意就是方程
的单调性,得极大值或极小值(极值点多时,最好列表表示);(3)题意就是方程![]() 无实数解,即关于
无实数解,即关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解.一般是分类讨论,
上没有实数解.一般是分类讨论, ![]() 时,无实数解,
时,无实数解, ![]() 时,方程变为
时,方程变为![]() ,因此可通过求函数
,因此可通过求函数![]() 的值域来求得
的值域来求得![]() 的范围.
的范围.
试题解析:(1)由![]() ,得
,得![]() .
.
又曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,
轴,
得![]() ,即
,即![]() ,解得
,解得![]() .
.
(2)![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() 为
为![]() 上的增函数,
上的增函数,
所以函数![]() 无极值.
无极值.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
, ![]() .
.
![]() ,
,![]() ;
; ![]() ,
,![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,无极大值.
,无极大值.
综上,当![]() 时,函数
时,函数![]() 无极小值
无极小值
当![]() ,
, ![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.
(3)当![]() 时,
时, ![]()
令![]() ,
,
则直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,
没有公共点,
等价于方程![]() 在
在![]() 上没有实数解.
上没有实数解.
假设![]() ,此时
,此时![]() ,
,  ,
,
又函数![]() 的图象连续不断,由零点存在定理,可知
的图象连续不断,由零点存在定理,可知![]() 在
在![]() 上至少有一解,与“方程
上至少有一解,与“方程![]() 在
在![]() 上没有实数解”矛盾,故
上没有实数解”矛盾,故![]() .
.
又![]() 时,
时, ![]() ,知方程
,知方程![]() 在
在![]() 上没有实数解.
上没有实数解.
所以![]() 的最大值为
的最大值为![]() .
.
解法二:
(1)(2)同解法一.
(3)当![]() 时,
时, ![]() .
.
直线![]() :
: ![]() 与曲线
与曲线![]() 没有公共点,
没有公共点,
等价于关于![]() 的方程
的方程![]() 在
在![]() 上没有实数解,即关于
上没有实数解,即关于![]() 的方程:
的方程:
![]() (*)
(*)
在![]() 上没有实数解.
上没有实数解.
①当![]() 时,方程(*)可化为
时,方程(*)可化为![]() ,在
,在![]() 上没有实数解.
上没有实数解.
②当![]() 时,方程(*)化为
时,方程(*)化为![]() .
.
令![]() ,则有
,则有![]() .
.
令![]() ,得
,得![]() ,
,
当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
当![]() 时,
时, ![]() ,同时当
,同时当![]() 趋于
趋于![]() 时,
时, ![]() 趋于
趋于![]() ,
,
从而![]() 的取值范围为
的取值范围为![]() .
.
所以当![]() 时,方程(*)无实数解, 解得
时,方程(*)无实数解, 解得![]() 的取值范围是
的取值范围是![]() .
.
综上,得![]() 的最大值为
的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人射击一次命中7~10环的概率如下表
命中环数
7
8
9
10
命中概率
0.16
0.19
0.28
0.24
计算这名射手在一次 射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解初三女生身高情况,某中学对初三女生身高情况进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别
频数
频率
145.5~149.5
1
0.02
149.5~153.5
4
0.08
153.5~157.5
20
0.40
157.5~161.5
15
0.30
161.5~165.5
8
0.16
165.5~169.5
m
n
合 计
M
N
(1)求出表中m,n,M,N所表示的数分别是多少?
(2)画出频率分布直方图;
(3)全体女生中身高在哪组范围内的人数最多? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了估计某人的射击技术情况,在他的训练记录中抽取50次检验,他的命中环数如下:10,5,5,8,7,8,6,9,7,8,6,6,5,6,7,8,10,9,7,9,8,7,6,5,9,9,8,8,5,8,6,7,6,9,6,8,8,8,6,7,6,8,107,10,8,7,7,9,5
(1)列出频率分布表
(2)画出频率分布的直方图. -
科目: 来源: 题型:
查看答案和解析>>【题目】为研究质量x(单位:g)对弹簧长度y(单位:cm)的影响,对不同质量的6根弹簧进行测量,得到如下数据:
x (g)
5
10
15
20
25
30
y (cm)
7.25
8.12
8.95
9.90
10.9
11.8
(1)画出散点图;
(2)如果散点图中的各点大致分布在一条直线的附近,求y与x之间的回归方程. ( 其中 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=1﹣3sinx
(1)画出上述函数的图象
(2)求上述函数的最大值、最小值和周期,并求这个函数取最大值、最小值的x值的集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了得到函数y=sin(2x﹣
 )的图象,可以将函数y=sin2x的图象( )
)的图象,可以将函数y=sin2x的图象( )
A.向右平移 个单位
个单位
B.向右平移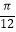 个单位
个单位
C.向左平移 个单位
个单位
D.向左平移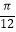 个单位
个单位
相关试题

