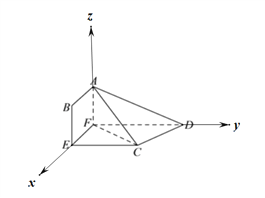
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,是否存在折叠后的线段
,是否存在折叠后的线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(![]() )求三棱锥
)求三棱锥![]() 的体积的最大值,并求此时点
的体积的最大值,并求此时点![]() 到平面
到平面![]() 的距离.
的距离.

参考答案:
【答案】(1)答案见解析;(2)答案见解析.
【解析】试题分析:
(1)存在![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() ,即
,即![]() ,利用几何关系可知四边形
,利用几何关系可知四边形![]() 为平行四边形,则
为平行四边形,则![]() ,利用线面平行的判断定理可知
,利用线面平行的判断定理可知![]() 平面
平面![]() 成立.
成立.
(2)由题意可得三棱锥![]() 的体积
的体积![]() ,由均值不等式的结论可知
,由均值不等式的结论可知![]() 时,三棱锥的体积
时,三棱锥的体积![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
建立空间直角坐标系,则![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,故点
,故点![]() 到平面
到平面![]() 的距离
的距离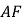 .
.
试题解析:
(![]() )存在
)存在![]() ,使得
,使得![]() 平面
平面![]() ,此时
,此时![]() .
.
证明:当![]() ,此时
,此时![]() ,
,
过![]() 作
作![]() ,与
,与![]() 交
交![]() ,则
,则![]() ,
,
又![]() ,故
,故![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,且
,且![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() 成立.
成立.
(![]() )∵平面
)∵平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
故三棱锥![]() 的体积
的体积![]() ,
,
∴![]() 时,三棱锥的体积
时,三棱锥的体积![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
建立如图所示的空间直角坐标系,则![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,
,
∴![]() ,取
,取![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() .
.
∴点![]() 到平面
到平面![]() 的距离
的距离 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
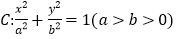 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的
,以原点为圆心,椭圆的短半轴长为半径的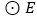 与直线
与直线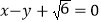 相切.
相切.(Ⅰ)求椭圆
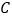 的方程;
的方程;(Ⅱ)过定点
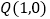 斜率为
斜率为 的直线与椭圆
的直线与椭圆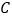 交于
交于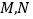 两点,若
两点,若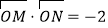 ,求斜率
,求斜率 的值;
的值;(Ⅲ)若(Ⅱ)中的直线
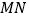 与
与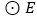 交于
交于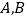 两点,设点
两点,设点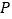 在
在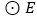 上,试探究使
上,试探究使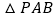 的面积为
的面积为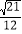 的点
的点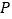 共有几个?证明你的结论.
共有几个?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是( )
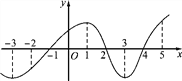
A. 在(-2,1)上f(x)是增函数 B. 在(1,3)上f(x)是减函数
C. 当x=2时,f(x)取极大值 D. 当x=4时,f(x)取极大值
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
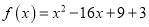 .
.(
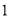 )若函数
)若函数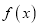 在
在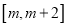 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.(
 )是否存在常数
)是否存在常数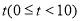 ,当
,当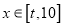 时,
时,  在值域为区间
在值域为区间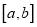 且
且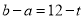 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】数学家欧拉1765年在其所著的《三角形几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标是( )
A. (-4,0) B. (0,-4) C. (4,0) D. (4,0)或(-4,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①“若
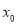 为
为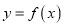 的极值点,则
的极值点,则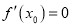 ”的逆命题为真命题;
”的逆命题为真命题; ②“平面向量
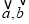 的夹角是钝角”的充分不必要条件是
的夹角是钝角”的充分不必要条件是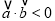
③若命题
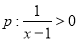 ,则
,则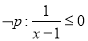
④函数
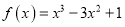 在点
在点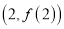 处的切线方程为
处的切线方程为 .
.其中不正确的个数是
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数

(1)若
 在
在 处取得极值,确定
处取得极值,确定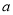 的值,并求此时曲线
的值,并求此时曲线 在点
在点 处的切线方程;
处的切线方程;(2)若
 在
在 上为减函数,求
上为减函数,求 的取值范围。
的取值范围。
相关试题

