【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的
,以原点为圆心,椭圆的短半轴长为半径的![]() 与直线
与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过定点![]() 斜率为
斜率为![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,若
两点,若![]() ,求斜率
,求斜率![]() 的值;
的值;
(Ⅲ)若(Ⅱ)中的直线![]() 与
与![]() 交于
交于![]() 两点,设点
两点,设点![]() 在
在![]() 上,试探究使
上,试探究使![]() 的面积为
的面积为![]() 的点
的点![]() 共有几个?证明你的结论.
共有几个?证明你的结论.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)见解析.
;(Ⅲ)见解析.
【解析】试题分析:(Ⅰ)运用椭圆的离心率公式和直线和圆相切的条件,结合![]() 的关系,解方程可得
的关系,解方程可得![]() ,进而得到椭圆方程;(Ⅱ)设直线
,进而得到椭圆方程;(Ⅱ)设直线![]() 方程为
方程为![]() ,代入椭圆方程,运用韦达定理和向量的数量积的坐标表示,解方程可得斜率
,代入椭圆方程,运用韦达定理和向量的数量积的坐标表示,解方程可得斜率![]() ;(Ⅲ)求得圆心到直线的距离,圆的弦长
;(Ⅲ)求得圆心到直线的距离,圆的弦长![]() ,由三角形的面积公式可得
,由三角形的面积公式可得![]() 到
到![]() 的距离,结合半径与圆心到直线的距离之差的关系,即可判断
的距离,结合半径与圆心到直线的距离之差的关系,即可判断![]() 的个数.
的个数.
试题解析:(Ⅰ)原点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
![]()
![]()
![]() 所以,椭圆
所以,椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)将直线![]() 与椭圆
与椭圆![]() 联立,消去
联立,消去![]() ,整理得
,整理得![]() ,由韦达定理得
,由韦达定理得![]() .
.
![]() .
.
![]() .
.
令![]() ,得
,得![]() .
.
(Ⅲ)由(2)知,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
原点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 弦长
弦长![]() .
.
若![]() 上存在点
上存在点![]() 使
使![]() 的面积为
的面积为![]() ,则点
,则点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() .
.
![]() 当直线
当直线![]() 的斜率
的斜率![]() 时,有4个点
时,有4个点![]() 使
使![]() 面积为
面积为![]() ;当直线
;当直线![]() 的斜率
的斜率![]() 时,有4个点
时,有4个点![]() 使
使![]() 面积为
面积为![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
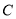 :
: 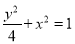 ,过点
,过点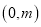 作圆
作圆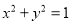 的切线交椭圆
的切线交椭圆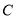 于
于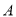 、
、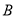 两点.
两点.(Ⅰ)求椭圆
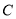 的焦点坐标和离心率;
的焦点坐标和离心率;(Ⅱ)将
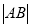 表示成
表示成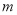 的函数,并求
的函数,并求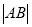 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
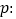 方程
方程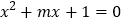 有两个不等的负根,
有两个不等的负根,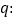 方程
方程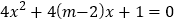 无实根,若“
无实根,若“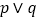 ”为真,“
”为真,“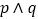 ”为假,求实数
”为假,求实数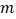 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【河南省新乡市2017届高三上学期第一次调研】设
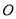 为坐标原点,已知椭圆
为坐标原点,已知椭圆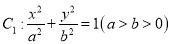 的离心率为
的离心率为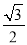 ,抛物线
,抛物线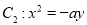 的准线方程为
的准线方程为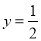 .
.(1)求椭圆
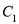 和抛物线
和抛物线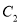 的方程;
的方程;(2)设过定点
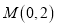 的直线
的直线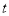 与椭圆
与椭圆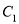 交于不同的两点
交于不同的两点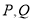 ,若
,若 在以
在以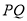 为直径的圆的外部,求直
为直径的圆的外部,求直线
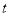 的斜率
的斜率 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是( )
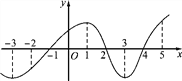
A. 在(-2,1)上f(x)是增函数 B. 在(1,3)上f(x)是减函数
C. 当x=2时,f(x)取极大值 D. 当x=4时,f(x)取极大值
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
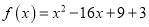 .
.(
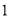 )若函数
)若函数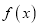 在
在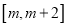 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.(
 )是否存在常数
)是否存在常数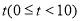 ,当
,当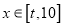 时,
时,  在值域为区间
在值域为区间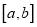 且
且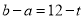 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中,  ,
,  ,
,  ,
,  ,
,  、
、 分别在
分别在 、
、 上,
上,  ,现将四边形
,现将四边形 沿
沿 折起,使平面
折起,使平面 平面
平面 .
.(
 )若
)若 ,是否存在折叠后的线段
,是否存在折叠后的线段 上存在一点
上存在一点 ,且
,且 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.(
 )求三棱锥
)求三棱锥 的体积的最大值,并求此时点
的体积的最大值,并求此时点 到平面
到平面 的距离.
的距离.
相关试题

