【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
参考答案:
【答案】(1)![]() ,切线方程为
,切线方程为![]() ;(2)
;(2)![]() .
.
【解析】
试题解析:本题考查求复合函数的导数,导数与函数的关系,由求导法则可得![]()
![]() ,由已知得
,由已知得![]() ,可得
,可得![]() ,于是有
,于是有![]()
![]() ,
,![]() ,
,![]() ,由点斜式可得切线方程;(2)由题意
,由点斜式可得切线方程;(2)由题意![]() 在
在![]() 上恒成立,即
上恒成立,即![]()
![]() 在
在![]() 上恒成立,利用二次函数的性质可很快得结论,由
上恒成立,利用二次函数的性质可很快得结论,由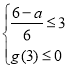 得
得![]() .
.
试题解析:(1)对![]() 求导得
求导得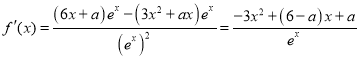
因为![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]() ,即
,即![]() .
.
当![]() 时,
时,![]()
![]() ,故
,故![]() ,从而
,从而![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,化简得
,化简得![]()
(2)由(1)得,![]() ,
,
令![]()
由![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,故
,故![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,故
,故![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,故
,故![]() 为减函数;
为减函数;
由![]() 在
在![]() 上为减函数,知
上为减函数,知![]() ,解得
,解得![]()
故a的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
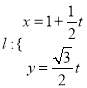 (
(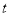 为参数),曲线
为参数),曲线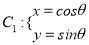 (
(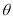 为参数).
为参数).(1)设
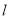 与
与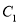 相交于
相交于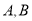 两点,求
两点,求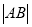 ;
;(2)若把曲线
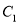 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的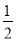 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的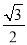 倍,得到曲线
倍,得到曲线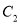 ,设点
,设点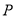 是曲线
是曲线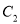 上的一个动点,求它到直线
上的一个动点,求它到直线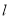 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】经国务院批复同意,郑州成功入围国家中心城市,某校学生团针对“郑州的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图1所示茎叶图.
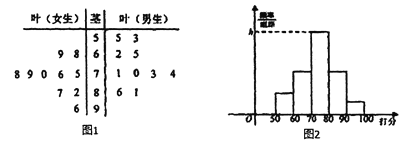
(1)分别计算男生女生打分的平均分,并用数学特征评价男女生打分的数据分布情况;
(2)如图2按照打分区间
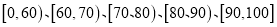 绘制的直方图中,求最高矩形的高;
绘制的直方图中,求最高矩形的高;(3)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
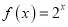 ,
, 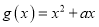 (其中
(其中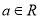 ).对于不相等的实数
).对于不相等的实数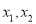 ,设
,设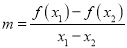 ,
, 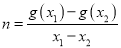 .现有如下命题:
.现有如下命题:(1)对于任意不相等的实数
 ,都有
,都有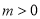 ;
;(2)对于任意的a及任意不相等的实数
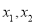 ,都有
,都有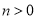 ;
;(3)对于任意的a,存在不相等的实数
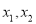 ,使得
,使得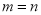 ;
;(4)对于任意的a,存在不相等的实数
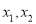 ,使得
,使得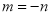 .
.其中的真命题有_____________(写出所有真命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列
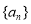 的前
的前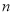 项和为
项和为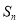 ,且
,且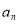 是
是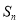 和
和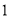 的等差中项,等差数列
的等差中项,等差数列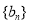 满足
满足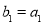 ,
,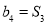 .
.(1)求数列
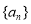 、
、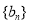 的通项公式;
的通项公式; (2)设
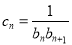 ,数列
,数列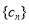 的前
的前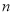 项和为
项和为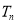 ,证明:
,证明: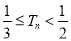 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
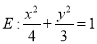 与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为
与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为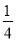 .
.(Ⅰ)证明直线AB恒过定点,并求定点的坐标;
(Ⅱ)求三角形ABM的面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=loga(1﹣
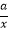 ),其中0<a<1.
),其中0<a<1.
(Ⅰ)证明:f(x)是(a,+∞)上的减函数;
(Ⅱ)若f(x)>1,求x的取值范围.
相关试题

