【题目】给出下列四个命题:
①“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真命题;
”的逆命题为真命题;
②“平面向量![]() 的夹角是钝角”的充分不必要条件是
的夹角是钝角”的充分不必要条件是![]()
③若命题![]() ,则
,则![]()
④函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
其中不正确的个数是
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】①“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为:若
”的逆命题为:若![]() 则
则![]() 为
为![]() 的极值点,这个命题是错误的,只有当
的极值点,这个命题是错误的,只有当![]() 是导函数的变号零点时才是极值点;故逆命题是假命题;
是导函数的变号零点时才是极值点;故逆命题是假命题;
②“平面向量![]() 的夹角是钝角”的充分不必要条件是
的夹角是钝角”的充分不必要条件是![]() ;这是假命题;向量夹角为钝角则
;这是假命题;向量夹角为钝角则![]() ,且向量夹角不为平角,故应是必要不充分条件;故是假命题;
,且向量夹角不为平角,故应是必要不充分条件;故是假命题;
③若命题![]() ,则
,则![]()
![]() 。故原命题是假命题;
。故原命题是假命题;
④函数![]() 在点
在点![]() 处的切线斜率为:0,
处的切线斜率为:0, ![]() ,故代入得到切线方程为:
,故代入得到切线方程为: ![]() .故为真命题;
.故为真命题;
故正确的只有一个④。其它三个均错。
故答案为:C。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
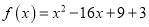 .
.(
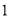 )若函数
)若函数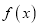 在
在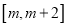 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.(
 )是否存在常数
)是否存在常数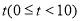 ,当
,当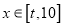 时,
时,  在值域为区间
在值域为区间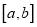 且
且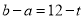 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中,  ,
,  ,
,  ,
,  ,
,  、
、 分别在
分别在 、
、 上,
上,  ,现将四边形
,现将四边形 沿
沿 折起,使平面
折起,使平面 平面
平面 .
.(
 )若
)若 ,是否存在折叠后的线段
,是否存在折叠后的线段 上存在一点
上存在一点 ,且
,且 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.(
 )求三棱锥
)求三棱锥 的体积的最大值,并求此时点
的体积的最大值,并求此时点 到平面
到平面 的距离.
的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家欧拉1765年在其所著的《三角形几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标是( )
A. (-4,0) B. (0,-4) C. (4,0) D. (4,0)或(-4,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数

(1)若
 在
在 处取得极值,确定
处取得极值,确定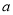 的值,并求此时曲线
的值,并求此时曲线 在点
在点 处的切线方程;
处的切线方程;(2)若
 在
在 上为减函数,求
上为减函数,求 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】若圆(x-1)2+(y+1)2=R2上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是( )
A. R>1 B. R<3 C. 1<R<3 D. R≠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥的底面半径为2,高为6,在其中有一个高为x的内接圆柱.
(1)用x表示圆柱的轴截面面积S;
(2)当x为何值时,S最大?
相关试题

