【题目】已知函数f(x)=(3﹣a)x﹣2+a﹣2lnx(a∈R)
(1)若函数y=f(x)在区间(1,3)上单调,求a的取值范围;
(2)若函数g(x)=f(x)﹣x在(0, ![]() )上无零点,求a的最小值.
)上无零点,求a的最小值.
参考答案:
【答案】
(1)解:f′(x)=3﹣a﹣ ![]() =
= ![]() ,
,
当a≥3时,有f′(x)<0,即函数f(x)在区间(1,3)上单调递减;
当a<3时,令f′(x)=0,得x= ![]() ,若函数y=f(x)在区间(1,3)单调,
,若函数y=f(x)在区间(1,3)单调,
则 ![]() ≤1或
≤1或 ![]() ≥3,解得:a≤1或
≥3,解得:a≤1或 ![]() ≤a<3,
≤a<3,
综上,a的范围是(﹣∞,1]∪[ ![]() ,+∞)
,+∞)
(2)解:x→0时,g(x)→+∞,
∴g(x)=(2﹣a)(x﹣1)﹣2lnx<0在区间(0, ![]() )上恒成立不可能,
)上恒成立不可能,
故要使函数g(x)在(0, ![]() )无零点,只需对任意的x∈(0,
)无零点,只需对任意的x∈(0, ![]() ),g(x)>0恒成立,
),g(x)>0恒成立,
即对x∈(0, ![]() ),a>2﹣
),a>2﹣ ![]() 恒成立,
恒成立,
令l(x)=2﹣ ![]() ,x∈(0,
,x∈(0, ![]() ),
),
则l′(x)=  ,
,
令m(x)=2lnx+ ![]() ﹣2,x∈(0,
﹣2,x∈(0, ![]() ),
),
则m′(x)= ![]() <0,
<0,
故m(x)在(0, ![]() )上递减,于是m(x)>m(
)上递减,于是m(x)>m( ![]() )=2﹣2ln2>0,
)=2﹣2ln2>0,
从而,l′(x)>0,于是l(x)在(0, ![]() )递增,
)递增,
∴l(x)<l( ![]() )=2﹣4ln2,
)=2﹣4ln2,
故要使a>2﹣ ![]() 恒成立,只需a∈[2﹣4ln2,+∞),
恒成立,只需a∈[2﹣4ln2,+∞),
综上,若函数g(x)=f(x)﹣x在(0, ![]() )上无零点,则a的最小值是2﹣4ln2
)上无零点,则a的最小值是2﹣4ln2
【解析】(1)求出函数的导数,通过讨论a的范围,判断导函数的符号,从而求出函数的单调区间即可;(2)问题转化为对x∈(0, ![]() ),a>2﹣
),a>2﹣ ![]() 恒成立,令l(x)=2﹣
恒成立,令l(x)=2﹣ ![]() ,x∈(0,
,x∈(0, ![]() ),根据函数的单调性求出a的范围即可.
),根据函数的单调性求出a的范围即可.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的极值与导数(求函数
在这个区间单调递减),还要掌握函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值)的相关知识才是答题的关键.
是极小值)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要建造一个容积为1 600立方米,深为4米的长方体无盖蓄水池,池壁的造价为每平方米200元,池底的造价为每平方米100元.
(1)把总造价y元表示为池底的一边长x米的函数;
(2)由于场地原因,蓄水池的一边长不能超过20米,问蓄水池的这个底边长为多少时总造价最低?总造价最低是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂今年拟举行促销活动,经调查测算,该厂产品的年销售量(即该厂的年产量)x(万件)与年促销费m(万元)(m≥0)满足x=3-
 .已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
.已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将今年该产品的利润y(万元)表示为年促销费m(万元)的函数;
(2)求今年该产品利润的最大值,此时促销费为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知右焦点为F(c,0)的椭圆M:
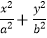 =1(a>b>0)过点
=1(a>b>0)过点 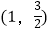 ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标是ρ=2asinθ,直线l的参数方程是
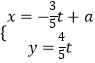 (t为参数).
(t为参数).
(1)若a=2,M为直线l与x轴的交点,N是圆C上一动点,求|MN|的最大值;
(2)若直线l被圆C截得的弦长为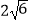 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设实数x、y满足2x+y=9.
(1)若|8﹣y|≤x+3,求x的取值范围;
(2)若x>0,y>0,求证: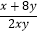 ≥
≥ 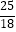 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆Γ:
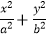 =1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y=
=1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y= 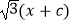 与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
相关试题

