【题目】椭圆Γ: ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y=
=1(a>b>0)的左右焦点分别为F1 , F2 , 焦距为2c,若直线y= ![]() 与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1 , 则该椭圆的离心率等于 .
参考答案:
【答案】![]()
【解析】解:如图所示,
由直线 ![]() 可知倾斜角α与斜率
可知倾斜角α与斜率 ![]() 有关系
有关系 ![]() =tanα,∴α=60°.
=tanα,∴α=60°.
又椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,∴ ![]() ,∴
,∴ ![]() .
.
设|MF2|=m,|MF1|=n,则 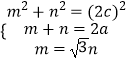 ,解得
,解得 ![]() .
.
∴该椭圆的离心率e= ![]() .
.
故答案为 ![]() .
.
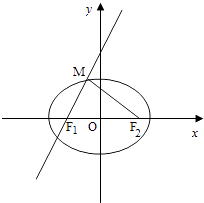
由直线 ![]() 可知斜率为
可知斜率为 ![]() ,可得直线的倾斜角α=60°.又直线与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1,可得
,可得直线的倾斜角α=60°.又直线与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1,可得 ![]() ,进而
,进而 ![]() .
.
设|MF2|=m,|MF1|=n,利用勾股定理、椭圆的定义及其边角关系可得 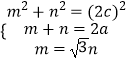 ,解出a,c即可.
,解出a,c即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(3﹣a)x﹣2+a﹣2lnx(a∈R)
(1)若函数y=f(x)在区间(1,3)上单调,求a的取值范围;
(2)若函数g(x)=f(x)﹣x在(0, )上无零点,求a的最小值.
)上无零点,求a的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标是ρ=2asinθ,直线l的参数方程是
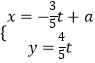 (t为参数).
(t为参数).
(1)若a=2,M为直线l与x轴的交点,N是圆C上一动点,求|MN|的最大值;
(2)若直线l被圆C截得的弦长为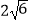 ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设实数x、y满足2x+y=9.
(1)若|8﹣y|≤x+3,求x的取值范围;
(2)若x>0,y>0,求证: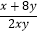 ≥
≥ 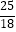 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ∈[1,+∞).
∈[1,+∞).(1)当
 时,判断函数
时,判断函数 的单调性并证明;
的单调性并证明;(2)当
 时,求函数
时,求函数 的最小值;
的最小值;(3)若对任意
 ∈[1,+∞),
∈[1,+∞), >0恒成立,试求实数
>0恒成立,试求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资
 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.(1)分别写出
 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程

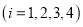 关于时间
关于时间 的函数关系式分别为
的函数关系式分别为 ,
, ,
, ,
,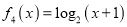 ,有以下结论:
,有以下结论:①当
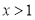 时,甲走在最前面;
时,甲走在最前面;②当
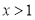 时,乙走在最前面;
时,乙走在最前面;③当
 时,丁走在最前面,当
时,丁走在最前面,当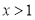 时,丁走在最后面;
时,丁走在最后面;④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为 (把正确结论的序号都填上,多填或少填均不得分).
相关试题

