【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响,已知某学生只选修甲的概率为0.08,只选修甲和乙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数![]() 为
为![]() 上的偶函数”为事件
上的偶函数”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)0.24
(2)
ξ | 0 | 2 |
P | 0.24 | 0.76 |
【解析】试题分析:(1)要想求事件![]() 的概率,由“函数
的概率,由“函数![]() 为
为![]() 上的奇函数”可知
上的奇函数”可知![]() ,将问题转化为“当
,将问题转化为“当![]() 时的概率”. 又因为
时的概率”. 又因为![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积,可将问题分为两种情况:该学生选修三门功课或三门功课都没选.不管哪种情况,都需要知道该学生选修甲、乙、丙的概率.所以,首先要求出该学生选修甲、乙、丙的概率.由题意可设该学生选修甲、乙、丙的概率分别为
表示该学生选修的课程门数和没有选修的课程门数的乘积,可将问题分为两种情况:该学生选修三门功课或三门功课都没选.不管哪种情况,都需要知道该学生选修甲、乙、丙的概率.所以,首先要求出该学生选修甲、乙、丙的概率.由题意可设该学生选修甲、乙、丙的概率分别为![]() 、
、![]() 、
、![]() ,联立方程组求解.再根据问题的两种情况进行求解.
,联立方程组求解.再根据问题的两种情况进行求解.
(2)因为![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积,分析可得以下2类对立事件:当选修三门功课或三门功课都没选时,
表示该学生选修的课程门数和没有选修的课程门数的乘积,分析可得以下2类对立事件:当选修三门功课或三门功课都没选时,![]() ;选修其中的一门时,
;选修其中的一门时,![]() .由(1)知
.由(1)知![]() 时的概率为
时的概率为![]() ,则
,则![]() 时的概率为
时的概率为![]() .可将
.可将![]() 的分布列写出,再计算出数学期望.
的分布列写出,再计算出数学期望.
试题解析:设该学生选修甲、乙、丙的概率分别为![]() 、
、![]() 、
、![]()
依题意得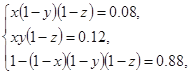
解得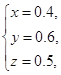
(1)若函数![]() 为
为![]() 的奇函数,则
的奇函数,则![]() .
.
当![]() 时,表示该学生选修三门功课或三门功课都没选.
时,表示该学生选修三门功课或三门功课都没选.
![]()
![]() 事件
事件![]() 的概率为
的概率为![]() .
.
(2)依题意知![]() 或
或![]() ,则
,则![]() 的分布列为
的分布列为
由(1)知![]()
![]()

![]() 的数学期望为
的数学期望为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
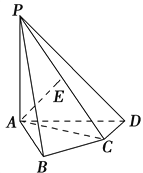
(1)证明:AE⊥平面PCD;
(2)求二面角A-PD-C的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△
 中,已知
中,已知 ,直线
,直线 经过点
经过点 .
.(Ⅰ)若直线
 :
: 与线段
与线段 交于点
交于点 ,且
,且 为△
为△ 的外心,求△
的外心,求△ 的外接圆的方程;
的外接圆的方程;(Ⅱ)若直线
 方程为
方程为 ,且△
,且△ 的面积为
的面积为 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了分析本校高中生的性别与是否喜欢数学之间的关系,在高中生中随机地抽取了90名学生调查,得到了如下列联表:
喜欢数学
不喜欢数学
总计
男
30
①
45
女
②
25
45
总计
③
④
90
(1)求①②③④处分别对应的值;
(2)能有多大把握认为“高中生的性别与喜欢数学”有关?
附:

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=2sin(ωx+
 )(ω>0)的图象向右平移
)(ω>0)的图象向右平移  个单位,得到函数y=g(x)的图象,若y=g(x)在[﹣
个单位,得到函数y=g(x)的图象,若y=g(x)在[﹣  ,
,  ]上为增函数,则ω的最大值为( )
]上为增函数,则ω的最大值为( )
A.3
B.2
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线C:
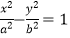 (a>0,b>0)的左、右焦点分别为F1 , F2 , 点M与双曲线C的焦点不重合,点M关于F1 , F2的对称点分别为A,B,线段MN的中点在双曲线的右支上,若|AN|﹣|BN|=12,则a=( )
(a>0,b>0)的左、右焦点分别为F1 , F2 , 点M与双曲线C的焦点不重合,点M关于F1 , F2的对称点分别为A,B,线段MN的中点在双曲线的右支上,若|AN|﹣|BN|=12,则a=( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】某生产企业研发了一种新产品,该产品在试销一个阶段后得到销售单价
 (单位:元)和销售量
(单位:元)和销售量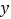 (单位:万件)之间的一组数据,如下表所示:
(单位:万件)之间的一组数据,如下表所示:销售单价
 /元
/元9
9.5
10
10.5
11
销售量
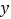 /万件
/万件11
10
8
6
5
(1)根据表中数据,建立
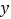 关于的
关于的 回归方程;
回归方程;(2)从反馈的信息来看,消费者对该产品的心理价(单位:元/件)在
 内,已知该产品的成本是
内,已知该产品的成本是 元/件(其中
元/件(其中 ),那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
),那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)参考数据:
 ,
, .
.参考公式:
 ,
, .
.
相关试题

