搜索
【题目】某生产企业研发了一种新产品，该产品在试销一个阶段后得到销售单价
（单位：元）和销售量
（单位：万件）之间的一组数据，如下表所示：
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量 | 11 | 10 | 8 | 6 | 5 |
（1）根据表中数据，建立关于的回归方程；
（2）从反馈的信息来看，消费者对该产品的心理价（单位：元/件）在
内，已知该产品的成本是
元/件（其中
），那么在消费者对该产品的心理价的范围内，销售单价定为多少时，企业才能获得最大利润？（注：利润=销售收入-成本）
参考数据：
，
.
参考公式：
，
.
参考答案：
【答案】（1）
；（2）见解析
【解析】分析：（1）根据表格计算
，进而根据公式得到
，从而得到
关于的
回归方程；
（2）利润
，即求二次函数的最值.
详解：（1）∵ 
，
∴ 
，
∴ 关于的回归方程为
；
（2）利润
，
，
∵ 
，该二次函数的对称轴方程
，
∴ ① 当
，即
时，函数在上单调递增，当
时
取得最大值；
② 
，即
时，当
时取得最大值；
∴ 当时，该产品的销售单价为
元时能获得最大利润；当时，该产品的销售单价为
元时能获得最大利润．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响，已知某学生只选修甲的概率为0.08，只选修甲和乙的概率是0.12，至少选修一门的概率是0.88，用
表示该学生选修的课程门数和没有选修的课程门数的乘积．（1）记“函数
为
上的偶函数”为事件
，求事件的概率；（2）求
的分布列和数学期望． -
科目： 来源： 题型：
查看答案和解析>>【题目】将函数f（x）=2sin（ωx+
）（ω＞0）的图象向右平移 
个单位，得到函数y=g（x）的图象，若y=g（x）在[﹣ 
， 
]上为增函数，则ω的最大值为（ ）
A.3
B.2
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知双曲线C：
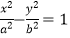（a＞0，b＞0）的左、右焦点分别为F1 ， F2 ， 点M与双曲线C的焦点不重合，点M关于F1 ， F2的对称点分别为A，B，线段MN的中点在双曲线的右支上，若|AN|﹣|BN|=12，则a=（ ）
A.3
B.4
C.5
D.6 -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学在“三关心”（即关心家庭、关心学校、关心社会）的专题中，对个税起征点问题进行了学习调查.学校决定从高一年级800人，高二年级1000人，高三年级800人中按分层抽样的方法共抽取13人进行谈话，其中认为个税起征点为3000元的有3人，认为个税起征点为4000元的有6人，认为个税起征点为 5000元的有4人.
（1）求高一年级、高二年级、高三年级分别抽取多少人？
（2）从13人中选出3人，求至少有1人认为个税起征点为4000元的概率；
（3）记从13人中选出3人中认为个税起征点为4000元的人数为
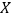，求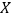的分布列与数学期望. -
科目： 来源： 题型：
查看答案和解析>>【题目】经市场调查，某种商品在进价基础上每涨价1元，其销售量就减少10个，已知这种商品进价为40元/个，若按50元一个售出时能卖出500个．
（1）请写出售价x（
）元与利润y元之间的函数关系式；（2）试计算当售价定为多少元时，获得的利润最大，并求出最大利润．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
（1）求函数
的值域；（2）若
时，函数的最小值为
，求
的值和函数的最大值．
相关试题
