练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥PABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．

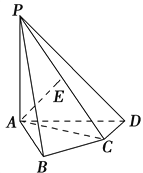
    (1)证明：AE⊥平面PCD；

    (2)求二面角A－PD－C的正弦值．

    【答案】（1）见解析；（2）.

    【解析】试题分析：（1）通过和得到 平面，利用等腰三角形的性质可得，可得结论；（2）过点作，垂足为，连接，证得是二面角的平面角，在中先求出，然后在中求出结论.

    试题解析：(1)证明：在四棱锥中，因底面， 平面，

    故.由条件， ，∴平面.

    又平面，∴.

    由， ，可得.

    ∵是的中点，∴.

    又，综上得平面.

    （2）过点作，垂足为，连接，

    由（1）知， 平面， 在平面内的射影是，则．

    因此是二面角的平面角．

    由已知，可得．设，可得， ，

    ， ．

    在中，∵，∴，则 ，

    在中， .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知点，圆的方程为，点为圆上的动点，过点的直线被圆截得的弦长为．

    (1)求直线的方程；

    (2)求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）（x∈R）满足f（x）=f（2-x），且对任意的x1，x2∈（-∞，1]（x1≠x2）有（x1-x2）（f（x1）-f（x2））＜0．则（　　）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，其中AD∥BC，AB⊥AD，AB=AD= BC， = ．
    （1）求证：DE⊥平面PAC；
    （2）若直线PE与平面PAC所成角的正弦值为 ，求二面角A﹣PC﹣D的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C的参数方程是 （θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，A、B的极坐标分别为A﹣（2，0）、B（﹣1， ）
    （1）求直线AB的直角坐标方程；
    （2）在曲线C上求一点M，使点M到AB的距离最大，并求出些最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线C： （a＞0，b＞0）的左、右焦点分别为F1 ， F2 ， 点M与双曲线C的焦点不重合，点M关于F1 ， F2的对称点分别为A，B，线段MN的中点在双曲线的右支上，若|AN|﹣|BN|=12，则a=（ ）
    A.3
    B.4
    C.5
    D.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题：

    ①圆与直线相交，所得弦长为；

    ②直线与圆恒有公共点；

    ③若棱长为的正方体的顶点都在同一球面上，则该球的表面积为；

    ④若棱长为的正四面体的顶点都在同一球面上，则该球的体积为.

    其中，正确命题的序号为__________．（写出所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}共有5项，其中a1=0，a5=2，且|ai+1﹣ai|=1，i=1，2，3，4，则满足条件的不同数列的个数为（　　）
    A.3
    B.4
    C.5
    D.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，面，，，，是棱上一点．

    （1）求证：；

    （2）若分别为、的中点，求证：//平面．

    查看答案和解析>>

    同步练习册答案