【题目】已知函数![]() .
.
(1)若![]() 是实数集
是实数集![]() 上的奇函数,求
上的奇函数,求![]() 的值;
的值;
(2)用定义证明![]() 在实数集
在实数集![]() 上单调递增;
上单调递增;
(3)若![]() 值域为
值域为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)根据奇函数性质f(x)+f(﹣x)= 0,化简可得![]() 的值;(2)关键在于作差之后的变形,一般先通分再因式分解,最后讨论各因子符号,进而确定差的符号(3)先根据函数单调性确定函数值域,再根据集合包含关系,利用数轴确定
的值;(2)关键在于作差之后的变形,一般先通分再因式分解,最后讨论各因子符号,进而确定差的符号(3)先根据函数单调性确定函数值域,再根据集合包含关系,利用数轴确定![]() 的取值范围.
的取值范围.
试题解析:(1)∵f(x)是R上的奇函数,
∴f(x)+f(﹣x)=m﹣![]() +m﹣
+m﹣![]() =0,即2m﹣(
=0,即2m﹣( ![]() +
+![]() )=02m﹣1=0,
)=02m﹣1=0,
解得m=![]() ;
;
(2)设 x1<x2且x1,x2∈R,
则f(x1)﹣f(x2)=m﹣![]() ﹣(m﹣
﹣(m﹣![]() )=
)=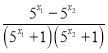 ,
,
∵x1<x2∴![]() ,
, ![]() ,
,
∴f(x1)﹣f(x2)<0,即f(x1)<f(x2),
∴f(x)在R上单调递增;
(3)由![]()
![]() ,所以m﹣1<f(x)<m,f(x)值域为D,且
,所以m﹣1<f(x)<m,f(x)值域为D,且![]()
∴D=(m﹣1,m),
∵![]()
∴,
![]() ∴m的取值范围是
∴m的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
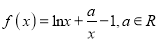 .
.(1)若函数
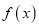 的最小值为
的最小值为 ,求
,求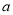 的值;
的值;(2)证明:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:

(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为
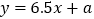 ,求
,求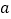 ,并估计
,并估计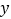 的预报值;
的预报值; (Ⅱ)现准备勘探新井
 ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的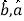 的值(
的值(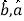 精确到0.01)相比于(Ⅰ)中
精确到0.01)相比于(Ⅰ)中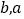 的值之差不超过10%,则使用位置最接近的已有旧井
的值之差不超过10%,则使用位置最接近的已有旧井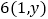 ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?(参考公式和计算结果:
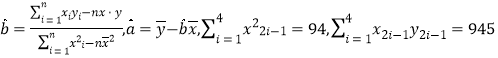 )
)(Ⅲ)设出油量与勘探深度的比值
 不低于20的勘探并称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探并称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数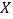 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
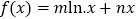 在点
在点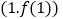 处的切线与直线
处的切线与直线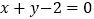 平行,且
平行,且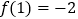 ,其中
,其中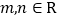 .
.(Ⅰ)求
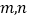 的值,并求出函数
的值,并求出函数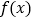 的单调区间;
的单调区间;(Ⅱ)设函数
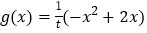 ,对于正实数
,对于正实数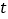 ,若
,若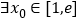 ,使得
,使得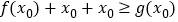 成立,求
成立,求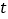 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
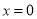 和
和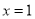 是函数
是函数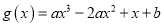 的两个零点,
的两个零点,(1)求实数
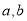 的值;
的值;(2)设
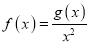
①若不等式
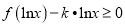 在
在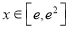 上恒成立,求实数
上恒成立,求实数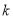 的取值范围;
的取值范围;②若
 有三个不同的实数解,求实数
有三个不同的实数解,求实数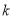 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(-x2+x-1)ex,其中e是自然对数的底数.
(1)求曲线f(x)在点(1,f(1))处的切线;
(2)若方程f(x)=
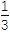 x3+
x3+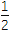 x2+m有3个不同的根,求实数m的取值范围.
x2+m有3个不同的根,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计划在某水库建一座至多安装
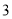 台发电机的水电站,过去
台发电机的水电站,过去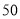 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量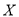 (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足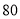 的年份有
的年份有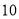 年,不低于
年,不低于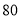 且不超过
且不超过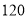 的年份有
的年份有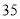 年,超过
年,超过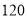 的年份有
的年份有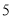 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.(1)求未来
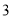 年中,设
年中,设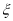 表示流量超过
表示流量超过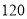 的年数,求
的年数,求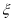 的分布列及期望;
的分布列及期望;(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量
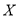 限制,并有如下关系:
限制,并有如下关系:年入流量
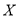
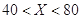
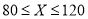
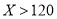
发电机最多可运行台数
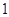
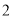
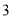
若某台发电机运行,则该台年利润为
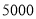 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损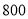 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
相关试题

