【题目】已知函数f(x)=(-x2+x-1)ex,其中e是自然对数的底数.
(1)求曲线f(x)在点(1,f(1))处的切线;
(2)若方程f(x)=![]() x3+
x3+![]() x2+m有3个不同的根,求实数m的取值范围.
x2+m有3个不同的根,求实数m的取值范围.
参考答案:
【答案】见解析
【解析】(1)因为f(x)=(-x2+x-1)ex,
所以f′(x)=(-2x+1)ex+(-x2+x-1)ex=(-x2-x)ex.
所以曲线f(x)在点(1,f(1))处的切线斜率为
k=f′(1)=-2e.
又f(1)=-e,
所以所求切线方程为y+e=-2e(x-1),即2ex+y-e=0.
(2)因为f′(x)=(-2x+1)ex+(-x2+x-1)ex=(-x2-x)ex,
当x<-1或x>0时,f′(x)<0;
当-1<x<0时,f′(x)>0,
所以f(x)=(-x2+x-1)ex在(-∞,-1)上单调递减,在(-1,0)上单调递增,在(0,+∞)上单调递减,
所以f(x)在x=-1处取得极小值f(-1)=-![]() ,在x=0处取得极大值f(0)=-1.
,在x=0处取得极大值f(0)=-1.
令g(x)=![]() x3+
x3+![]() x2+m,得g′(x)=x2+x.
x2+m,得g′(x)=x2+x.
当x<-1或x>0时,g′(x)>0;
当-1<x<0时,g′(x)<0,
所以g(x)在(-∞,-1)上单调递增,在(-1,0)上单调递减,在(0,+∞)上单调递增.
故g(x)在x=-1处取得极大值g(-1)=![]() +m,在x=0处取得极小值g(0)=m.
+m,在x=0处取得极小值g(0)=m.
因为方程f(x)=![]() x3+
x3+![]() x2+m有3个不同的根,
x2+m有3个不同的根,
即函数f(x)与g(x)的图象有3个不同的交点,
所以![]() ,即
,即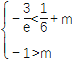 .
.
所以-![]() -
-![]() <m<-1.
<m<-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
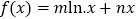 在点
在点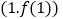 处的切线与直线
处的切线与直线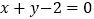 平行,且
平行,且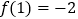 ,其中
,其中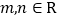 .
.(Ⅰ)求
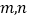 的值,并求出函数
的值,并求出函数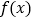 的单调区间;
的单调区间;(Ⅱ)设函数
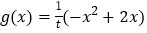 ,对于正实数
,对于正实数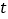 ,若
,若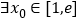 ,使得
,使得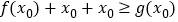 成立,求
成立,求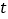 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
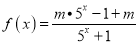 .
.(1)若
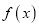 是实数集
是实数集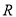 上的奇函数,求
上的奇函数,求 的值;
的值;(2)用定义证明
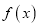 在实数集
在实数集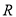 上单调递增;
上单调递增;(3)若
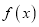 值域为
值域为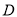 ,且
,且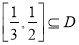 ,求
,求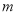 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
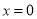 和
和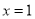 是函数
是函数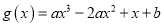 的两个零点,
的两个零点,(1)求实数
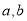 的值;
的值;(2)设
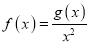
①若不等式
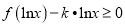 在
在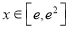 上恒成立,求实数
上恒成立,求实数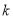 的取值范围;
的取值范围;②若
 有三个不同的实数解,求实数
有三个不同的实数解,求实数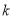 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计划在某水库建一座至多安装
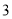 台发电机的水电站,过去
台发电机的水电站,过去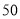 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量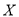 (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足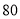 的年份有
的年份有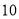 年,不低于
年,不低于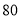 且不超过
且不超过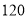 的年份有
的年份有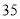 年,超过
年,超过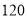 的年份有
的年份有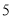 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.(1)求未来
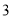 年中,设
年中,设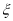 表示流量超过
表示流量超过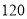 的年数,求
的年数,求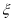 的分布列及期望;
的分布列及期望;(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量
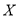 限制,并有如下关系:
限制,并有如下关系:年入流量
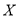
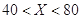
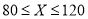
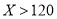
发电机最多可运行台数
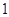
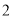
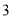
若某台发电机运行,则该台年利润为
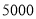 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损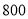 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
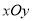 中,曲线
中,曲线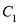 的参数方程为
的参数方程为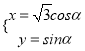 (
(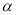 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以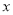 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线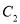 的极坐标方程为
的极坐标方程为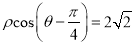 .
.(1)求曲线
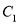 的普通方程和直线
的普通方程和直线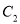 的直角坐标方程;
的直角坐标方程;(2)设点
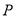 在
在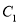 上,点
上,点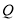 在
在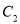 上,求
上,求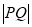 的最小值及对应的点
的最小值及对应的点 的直角坐标.
的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】微信是现代生活进行信息交流的重要工具,若要调查某公司使用微信的员工经常使用微信与年龄的关系,并规定每天使用微信时间在一小时以上为经常使用微信。据统计,该公司200名员工中90%的人使用微信,其中不经常使用微信的有60人,其余经常使用微信。若将员工年龄分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,使用微信的中75%是青年人.经常使用微信的员工中,有80人是青年人.
(1)请完成如下
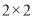 联列表,
联列表,青年人
中年人
合计
经常使用微信
不经常使用微信
合计
(2)由列联表中所得数据,是否有99.9%的把握认为“经常使用微信与年龄有关”?
(3)现采用分层抽样的方法从“经常使用微信的人”中抽取6人,从已抽取的这6人中任选2人,求“选出的2人均为青年人”的概率.
相关试题

