【题目】某企业生产某种产品时的能耗y与产品件数x之间的关系式为y=ax+![]() .且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
.且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
(1)写出函数y关于x的解析式;
(2)用列表法表示此函数,并画出图象.
参考答案:
【答案】(1) ![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)将x=2时,y=100;x=7时,y=35代入解析式,列方程组求出a和b,可写出函数y关于x的解析式;(2)根据定义域列出函数上的各点,在平面直角坐标系中描出这些点,即函数的图象.
试题解析:
(1)将![]()
![]() 代入y=ax+
代入y=ax+![]() 中,
中,
得
![]()
![]()
所以所求函数解析式为![]() .
.
(2)当x∈{1,2,3,4,5,…,20}时,列表:
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
y | 197 | 100 | 68.3 | 53 | 44.2 | 38.7 | 35 | 32.5 | 30.8 | 29.6 |
x | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
y | 28.8 | 28.3 | 28.1 | 28 | 28.1 | 28.25 | 28.5 | 28.9 | 29.3 | 29.8 |
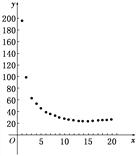
依据上表,画出函数y的图象如图所示,由20个点构成的点列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:
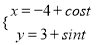 (t为参数)曲线C2:
(t为参数)曲线C2: +y2=4.
+y2=4.(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换
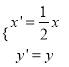 后得到曲线C′。求曲线C′的普通方程,并写出它的参数方程;
后得到曲线C′。求曲线C′的普通方程,并写出它的参数方程;(2)若C1上的点P对应的参数为t=π/2,Q为C′上的动点,求PQ中点M到直线C3:
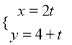 (t为参数)的距离的最小值
(t为参数)的距离的最小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
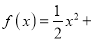
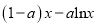 ,
, 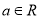 .
.(1)若
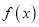 存在极值点1,求
存在极值点1,求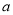 的值;
的值;(2)若
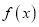 存在两个不同的零点,求证:
存在两个不同的零点,求证: 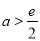 (
(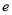 为自然对数的底数,
为自然对数的底数, 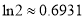 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
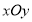 中,直线
中,直线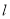 的方程为
的方程为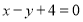 ,曲线
,曲线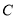 的参数方程为
的参数方程为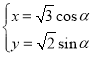 (
(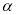 为参数).
为参数).(1)已知在极坐标系(与直角坐标系
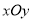 取相同的长度单位,且以原点
取相同的长度单位,且以原点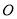 为极点,以
为极点,以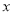 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点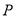 的极坐标为
的极坐标为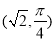 ,判断点
,判断点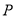 与曲线
与曲线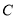 的位置关系;
的位置关系;(2)设点
 是曲线
是曲线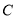 上的一个动点,求它到直线
上的一个动点,求它到直线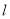 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知函数f(x)的定义域为[0,1],求f(x2+1)的定义域;
(2)已知f(
 )的定义域为[0,3],求f(x)的定义域.
)的定义域为[0,3],求f(x)的定义域. -
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ-
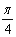 )=
)=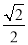 .
.(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
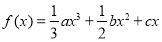 (
(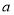 ,
,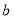 ,
,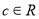 ,
,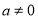 )的图象在点
)的图象在点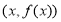 处的切线的斜率为
处的切线的斜率为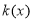 ,且函数
,且函数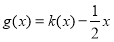 为偶函数.若函数
为偶函数.若函数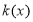 满足下列条件:①
满足下列条件:①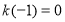 ;②对一切实数
;②对一切实数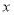 ,不等式
,不等式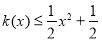 恒成立.
恒成立.(1)求函数
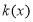 的表达式;
的表达式;(2)设函数
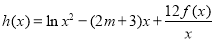 (
(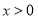 )的两个极值点
)的两个极值点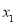 ,
,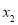 (
(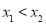 )恰为
)恰为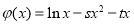 的零点,当
的零点,当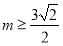 时,求
时,求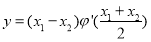 的最小值.
的最小值.
相关试题

