【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数![]() 在
在![]() 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)不是,理由见解析;(2)![]() .
.
【解析】
试题分析:(1)当![]() 时,函数
时,函数![]() ,换元后根据复合函数单调性求得函数值域为
,换元后根据复合函数单调性求得函数值域为![]() ,故不存在;(2)依题意有
,故不存在;(2)依题意有![]() ,即
,即![]() ,令
,令![]() 换元后分离参数,利用基本不等式和函数的单调性求得实数
换元后分离参数,利用基本不等式和函数的单调性求得实数![]() 的取值范围.
的取值范围.
试题解析:
(1)当![]() 时,
时,![]() ,令
,令![]() ,∵
,∵![]() ,∴
,∴![]() ,
,![]() ;
;
∵![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,即
,即![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
故不存在常数![]() ,使
,使![]() 成立.∴函数
成立.∴函数![]() 在
在![]() 上不是有界函数.…………………………6分
上不是有界函数.…………………………6分
(2)由题意知,![]() 对
对![]() 恒成立,
恒成立,
即:![]() ,令
,令![]() ,∵
,∵![]() ,∴
,∴![]() .
.
∴![]() 对
对![]() 恒成立,∴
恒成立,∴![]() ,
,
设![]() ,
,![]() ,由
,由![]() ,
,
由于![]() 在
在![]() 上递增,
上递增,![]() 在
在![]() 上递减,
上递减,
![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .……………………12分
.……………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
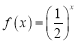 ,函数
,函数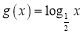 .
.⑴若
 的定义域为
的定义域为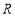 ,求实数
,求实数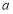 的取值范围;
的取值范围;⑵当
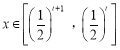 时,求函数
时,求函数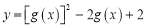 的最小值
的最小值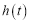 ;
;⑶是否存在非负实数
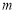 、
、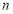 ,使得函数
,使得函数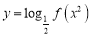 的定义域为
的定义域为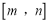 ,值域为
,值域为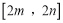 ,若存在,求出
,若存在,求出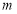 、
、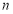 的值;若不存在,则说明理由.
的值;若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题“若a、b∈N,ab能被2整除,则a,b中至少有一个能被2整除”,那么反设的内容是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若0<a<1,b>0则函数f(x)=ax+b的图象一定经过( )
A. 第一、二象限 B. 第二、四象限
C. 第一、二、四象限 D. 第二、三、四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
B.在线性回归分析中,相关系数r的值越大,变量间的相关性越强
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.在回归分析中,
 为0.98的模型比
为0.98的模型比 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体
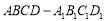 中,棱长
中,棱长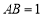 ,过点
,过点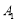 的平面
的平面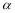 与正方体的面相交,交线围成一个正三角形.
与正方体的面相交,交线围成一个正三角形.
(1)在图中画出这个正三角形(不必说明画法和理由);
(2)平面
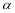 将该正方体截成两个几何体,求体积较大的几何体的体积和表面积.
将该正方体截成两个几何体,求体积较大的几何体的体积和表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是偶函数.
是偶函数.(1)求
 的值;
的值;(2)若函数
 ,是否存在实数
,是否存在实数 使得
使得 最小值为0,若存在,求出
最小值为0,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

