【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,cosB=![]() .
.
(Ⅰ)若c=2a,求![]() 的值;
的值;
(Ⅱ)若C-B=![]() ,求sinA的值.
,求sinA的值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由余弦定理结合![]() ;可得
;可得![]() ,再由正弦定理可得结果;(2)先由
,再由正弦定理可得结果;(2)先由![]() ,根据二倍角公式可得
,根据二倍角公式可得![]() ,则
,则![]() ,根据两角差的正弦公式可得结果.
,根据两角差的正弦公式可得结果.
试题解析:(1)解法1
在△ABC中,因为cosB=![]() ,所以
,所以![]() =
=![]() .
.
因为c=2a,所以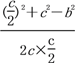 =
=![]() ,即
,即![]() =
=![]() ,
,
所以![]() =
=![]() .
.
又由正弦定理得![]() =
=![]() ,
,
所以![]() =
=![]() .
.
解法2
因为cosB=![]() ,B∈(0,),所以sinB=
,B∈(0,),所以sinB=![]() =
=![]() .
.
因为c=2a,由正弦定理得sinC=2sinA,
所以sinC=2sin(B+C)=![]() cosC+
cosC+![]() sinC,
sinC,
即-sinC=2cosC.
又因为sin2C+cos2C=1,sinC>0,解得sinC=![]() ,
,
所以![]() =
=![]() .
.
(2)因为cosB=![]() ,所以cos2B=2cos2B-1=
,所以cos2B=2cos2B-1=![]() .
.
又0<B<π,所以sinB=![]() =
=![]() ,
,
所以sin2B=2sinBcosB=2×![]() ×
×![]() =
=![]() .
.
因为C-B=![]() ,即C=B+
,即C=B+![]() ,所以A=π-(B+C)=
,所以A=π-(B+C)=![]() -2B,
-2B,
所以sinA=sin(![]() -2B)
-2B)
=sin![]() cos2B-cos
cos2B-cos![]() sin2B
sin2B
=![]() ×
×![]() -(-
-(-![]() )×
)×![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组函数中,表示相等函数的一组是( )
A.f(x)=|x|,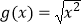
B.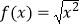 ,
, 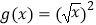
C.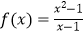 ,g(x)=x+1
,g(x)=x+1
D.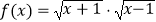 ,
, 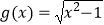
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
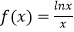
(1)求函数f(x)的单调区间;
(2)设a>0,求函数f(x)在[2a,4a]上的最小值;
(3)某同学发现:总存在正实数a、b(a<b),使ab=ba , 试问:他的判断是否正确?若不正确,请说明理由;若正确,请直接写出a的取值范围(不需要解答过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】(1).选修4—1:几何证明选讲
如图,CD是圆O的切线,切点为D,CA是过圆心O的割线且交圆O于点B,DA=DC.求证: CA=3CB.
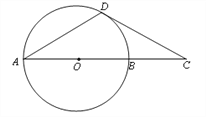
(2).选修4—2:矩阵与变换
设二阶矩阵A=
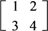 .
.(Ⅰ)求A-1;
(Ⅱ)若曲线C在矩阵A对应的变换作用下得到曲线C:6x2-y2=1,求曲线C的方程.
(3).选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为
 (t为参数),圆C的参数方程为
(t为参数),圆C的参数方程为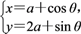 (θ为参数).若直线l与圆C相切,求实数a的值.
(θ为参数).若直线l与圆C相切,求实数a的值.(4).选修4—5:不等式选讲
解不等式:|x-2|+|x+1|≥5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x||x+1|<1},B={x|y=
 ,y∈R},则A∩RB=( )
,y∈R},则A∩RB=( )
A.(﹣2,1)
B.(﹣2,﹣1]
C.(﹣1,0)
D.[﹣1,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
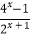 ,则下列关于函数f(x)的说法正确的是( )
,则下列关于函数f(x)的说法正确的是( )
A.为奇函数且在R上为增函数
B.为偶函数且在R上为增函数
C.为奇函数且在R上为减函数
D.为偶函数且在R上为减函数 -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知函数f(x)=2x3-3(a+1)x2+6ax,a∈R.
(Ⅰ)曲线y=f(x)在x=0处的切线的斜率为3,求a的值;
(Ⅱ)若对于任意x∈(0,+∞),f(x)+f(-x)≥12lnx恒成立,求a的取值范围;
(Ⅲ)若a>1,设函数f(x)在区间[1,2]上的最大值、最小值分别为M(a)、m(a),
记h(a)=M(a)-m(a),求h(a)的最小值.
相关试题

