【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.

(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长.
的长.
参考答案:
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)先证明![]() 面
面![]() 可得
可得![]() ;(2)连接
;(2)连接![]() 交
交![]() 于点
于点![]() ,根据几何知识可得可得
,根据几何知识可得可得![]() ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得![]() 平面
平面![]() ;(3)建立空间直角坐标系,利用向量,通过计算求
;(3)建立空间直角坐标系,利用向量,通过计算求![]() 的长。
的长。
试题解析:(I)∵![]() 平面
平面![]() ,
, ![]() 面
面![]() ,
,
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() 中,
中, ![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() 面
面![]() .
.
∵![]() 面
面![]() ,
,
∴![]() .
.
(II)连接![]() 交
交![]() 于点
于点![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() 是
是![]() 的中点.
的中点.
又∵![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
又![]() 平面
平面![]() ,
, ![]() 面
面![]() ,
,
∴![]() 平面
平面![]() .
.
(III)∵![]() ,且
,且![]() 平面
平面![]() ,
,
∴![]() ,
, ![]() ,
, ![]() 两两垂直。
两两垂直。
以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
故![]() ,
, ![]() ,
,
则有![]() ,令
,令![]() ,则
,则![]() ,
,
又平面![]() 的法向量为
的法向量为![]() .
.
∵二面角![]() 的大小为
的大小为![]() ,
,
∴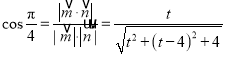 ,
,
解得![]() ,即
,即![]() ,
,
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆
 的离心率为
的离心率为 ,过左焦点
,过左焦点 且斜率为
且斜率为 的直线交椭圆
的直线交椭圆 于
于 ,
,  两点,线段
两点,线段 的中点为
的中点为 ,直线
,直线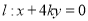 交椭圆
交椭圆 于
于 ,
,  两点.
两点.(I)求椭圆
 的方程.
的方程.(II)求证:点
 在直线
在直线 上.
上.(III)是否存在实数
 ,使得
,使得 的面积是
的面积是 面积的
面积的 倍?若存在,求出
倍?若存在,求出 的值.若不存在,说明理由.
的值.若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是空间两条直线,
是空间两条直线,  是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )A. 当
 时,“
时,“ ”是“
”是“ ”的充要条件
”的充要条件B. 当
 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件C. 当
 时,“
时,“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件D. 当
 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2+2x﹣3<0},集合B={x||x+a|<1}.
(1)若a=3,求A∪B;
(2)设命题p:x∈A,命题q:x∈B,若p是q成立的必要不充分条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:方程
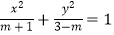 表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)判断函数f(x)的奇偶性,并证明;
(2)利用函数单调性的定义证明:f(x)是其定义域上的增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x﹣
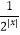 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
相关试题

