【题目】已知函数 ![]() .
.
(1)判断函数f(x)的奇偶性,并证明;
(2)利用函数单调性的定义证明:f(x)是其定义域上的增函数.
参考答案:
【答案】
(1)解:f(x)为奇函数.证明如下:
∵2x+1≠0,
∴f(x)的定义域为R,
又∵ ![]() ,
,
∴f(x)为奇函数
(2)解: ![]() ,
,
任取x1、x2∈R,设x1<x2,
∵ ![]() =
= ![]() =
= ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,又
,又 ![]() ,
, ![]() ,
,
∴f(x1)﹣f(x2)<0,∴f(x1)<f(x2).
∴f(x)在其定义域R上是增函数
【解析】(1)根据函数奇偶性的定义可作出判断、证明;(2) ![]() ,任取x1、x2∈R,设x1<x2 , 通过作差证明f(x1)<f(x2)即可;
,任取x1、x2∈R,设x1<x2 , 通过作差证明f(x1)<f(x2)即可;
【考点精析】通过灵活运用函数的单调性和奇偶性与单调性的综合,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种;奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2+2x﹣3<0},集合B={x||x+a|<1}.
(1)若a=3,求A∪B;
(2)设命题p:x∈A,命题q:x∈B,若p是q成立的必要不充分条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中,  底面
底面 ,
,  ,
,  ,
,  ,
,  是棱
是棱 上一点.
上一点.
(I)求证:
 .
.(II)若
 ,
,  分别是
分别是 ,
,  的中点,求证:
的中点,求证:  平面
平面 .
.(III)若二面角
 的大小为
的大小为 ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:方程
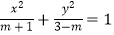 表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x﹣
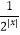 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于四面体ABCD,以下命题中,真命题的序号为(填上所有真命题的序号)
①若AB=AC,BD=CD,E为BC中点,则平面AED⊥平面ABC;
②若AB⊥CD,BC⊥AD,则BD⊥AC;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以A为端点的三条棱所在直线两两垂直,则A在平面BCD内的射影为△BCD的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数
 ,x∈[0,9]的值域为集合B,
,x∈[0,9]的值域为集合B,
(1)求A∩B;
(2)若C={x|3x<2m﹣1},且(A∩B)C,求实数m的取值范围.
相关试题

