【题目】已知命题p:方程 ![]() 表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
参考答案:
【答案】解:∵方程 ![]() 表示焦点在y轴上的椭圆, ∴0<m+1<3﹣m,
表示焦点在y轴上的椭圆, ∴0<m+1<3﹣m,
解得:﹣1<m<1,
∴若命题p为真命题,求实数m的取值范围是(﹣1,1);
若关于x的方程x2+2mx+2m+3=0无实根,则判别式△=4m2﹣4(2m+3)<0,
即m2﹣2m﹣3<0,得﹣1<m<3.
若“p∧q”为假命题,“p∨q”为真命题,则p,q为一个真命题,一个假命题,
若p真q假,则 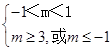 ,此时无解,
,此时无解,
柔p假q真,则 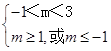 ,得1≤m<3.
,得1≤m<3.
综上,实数m的取值范围是[1,3)
【解析】若“p∧q”为假命题,“p∨q”为真命题,则p,q为一个真命题,一个假命题,进而可得实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是空间两条直线,
是空间两条直线,  是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )A. 当
 时,“
时,“ ”是“
”是“ ”的充要条件
”的充要条件B. 当
 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件C. 当
 时,“
时,“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件D. 当
 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|x2+2x﹣3<0},集合B={x||x+a|<1}.
(1)若a=3,求A∪B;
(2)设命题p:x∈A,命题q:x∈B,若p是q成立的必要不充分条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中,  底面
底面 ,
,  ,
,  ,
,  ,
,  是棱
是棱 上一点.
上一点.
(I)求证:
 .
.(II)若
 ,
,  分别是
分别是 ,
,  的中点,求证:
的中点,求证:  平面
平面 .
.(III)若二面角
 的大小为
的大小为 ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)判断函数f(x)的奇偶性,并证明;
(2)利用函数单调性的定义证明:f(x)是其定义域上的增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x﹣
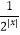 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于四面体ABCD,以下命题中,真命题的序号为(填上所有真命题的序号)
①若AB=AC,BD=CD,E为BC中点,则平面AED⊥平面ABC;
②若AB⊥CD,BC⊥AD,则BD⊥AC;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以A为端点的三条棱所在直线两两垂直,则A在平面BCD内的射影为△BCD的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面.
相关试题

