【题目】已知函数f(x)=2x﹣ ![]() .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:当x≤0时f(x)=0,
当x>0时, ![]() ,
,
有条件可得, ![]() ,
,
即22x﹣2×2x﹣1=0,解得 ![]() ,∵2x>0,∴
,∵2x>0,∴ ![]() ,∴
,∴ ![]() .
.
(2)解:当t∈[1,2]时, ![]() ,
,
即m(22t﹣1)≥﹣(24t﹣1).∵22t﹣1>0,∴m≥﹣(22t+1).
∵t∈[1,2],∴﹣(1+22t)∈[﹣17,﹣5],
故m的取值范围是[﹣5,+∞).
【解析】(1)当x≤0时得到f(x)=0而f(x)=2,所以无解;当x>0时解出f(x)=2求出x即可;(2)由 t∈[1,2]时,2tf(2t)+mf(t)≥0恒成立得到,得到f(t)= ![]() ,代入得到m的范围即可.
,代入得到m的范围即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,
中,  底面
底面 ,
,  ,
,  ,
,  ,
,  是棱
是棱 上一点.
上一点.
(I)求证:
 .
.(II)若
 ,
,  分别是
分别是 ,
,  的中点,求证:
的中点,求证:  平面
平面 .
.(III)若二面角
 的大小为
的大小为 ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:方程
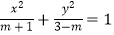 表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)判断函数f(x)的奇偶性,并证明;
(2)利用函数单调性的定义证明:f(x)是其定义域上的增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于四面体ABCD,以下命题中,真命题的序号为(填上所有真命题的序号)
①若AB=AC,BD=CD,E为BC中点,则平面AED⊥平面ABC;
②若AB⊥CD,BC⊥AD,则BD⊥AC;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以A为端点的三条棱所在直线两两垂直,则A在平面BCD内的射影为△BCD的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lg(x2﹣x﹣2)的定义域为集合A,函数
 ,x∈[0,9]的值域为集合B,
,x∈[0,9]的值域为集合B,
(1)求A∩B;
(2)若C={x|3x<2m﹣1},且(A∩B)C,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为
 ,这两条曲线在第一象限的交点为
,这两条曲线在第一象限的交点为 ,
,  是以
是以 为底边的等腰三角形.若
为底边的等腰三角形.若 ,记椭圆与双曲线的离心率分别为
,记椭圆与双曲线的离心率分别为 ,则
,则 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

