【题目】对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使![]() =
=![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
⑴当![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 内有两个不同的不动点,求实数
内有两个不同的不动点,求实数![]() 的取值范围;
的取值范围;
(3)若对于任意实数![]() ,函数
,函数![]() 恒有两个不相同的不动点,求实数
恒有两个不相同的不动点,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)f(x)的不动点为-1,2;(2)-4<b<4或4<b<6;(3)0<a<2.
【解析】试题分析:本题为新定义信息题,把a=2,b=-2代入后得到函数f(x)的解析式,假设存在不动点,根据不动点定义,满足![]() ,解方程求出不动点;当
,解方程求出不动点;当![]() 时,函数
时,函数![]() 在
在![]() 内有两个不同的不动点,说明方程在区间(-2,3)内有两个不等式实数根;同理解决第三步.
内有两个不同的不动点,说明方程在区间(-2,3)内有两个不等式实数根;同理解决第三步.
试题解析:
(1)当a=2,b=-2时,f(x)=2x2-x-4
∴ 由f(x)=x得x2-x-2=0, ∴ x=-1或x=2.
∴ f(x)的不动点为-1,2.
(2) 当a=2时,f(x)=2x2+(b+1)x+b-2,
由题意得f(x)=x在(-2,3)内有两个不同的不动点,
即方程 2x2+bx+b-2=0 在(-2,3)内的两个不相等的实数根.
设 g(x)=2x2+bx+b-2,
∴ 只须满足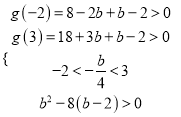 ∴
∴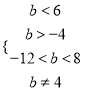
∴ -4<b<4或4<b<6
(3)由题意得:对于任意实数b,方程 ax2+bx+b-2=0总有两个不相等的实数解.
∴ ![]() ∴ b2-4ab+8a>0对b∈R恒成立.
∴ b2-4ab+8a>0对b∈R恒成立.
∴16a2-32a<0 ∴ 0<a<2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,动点
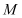 到定点
到定点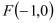 的距离和它到直线
的距离和它到直线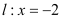 的距离
的距离之比是常数
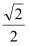 ,记动点
,记动点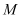 的轨迹为
的轨迹为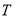 .
.(1)求轨迹
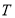 的方程;
的方程;(2)过点
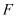 且不与
且不与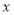 轴重合的直线
轴重合的直线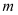 ,与轨迹
,与轨迹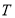 交于
交于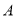 ,
,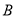 两点,线段
两点,线段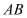 的垂直平分线与
的垂直平分线与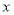 轴交于点
轴交于点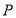 ,与轨迹
,与轨迹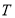 是否存在点
是否存在点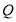 ,使得四边形
,使得四边形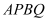 为菱形?若存在,请求出直线
为菱形?若存在,请求出直线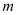 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1,求函数f(x)的解析式.
(2)已知x+y=12,xy=9且x<y,求
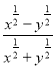 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为
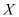 ,求
,求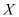 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在非零实数集上的函数
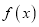 满足:
满足: 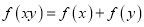 ,且
,且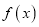 在区间
在区间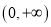 上为递增函数.
上为递增函数.(1)求
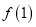 、
、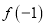 的值;
的值;(2)求证:
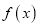 是偶函数;
是偶函数;(3)解不等式
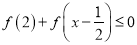 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
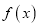 的定义域为D,若函数
的定义域为D,若函数 满足条件:存在
满足条件:存在 ,使
,使 在
在 上的值域为
上的值域为 ,则称
,则称 为“倍缩函数”,若函数
为“倍缩函数”,若函数 为“倍缩函数”,则实数
为“倍缩函数”,则实数 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

