【题目】在平面直角坐标系中,动点![]() 到定点
到定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离
的距离
之比是常数![]() ,记动点
,记动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() ,与轨迹
,与轨迹![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,与轨迹
,与轨迹![]() 是否存在点
是否存在点![]() ,使得四边形
,使得四边形![]() 为菱形?若存在,请求出直线
为菱形?若存在,请求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)直接根据题设条件列出等式,再进行化简,即可得到动点![]() 的轨迹
的轨迹![]() 的方程;(2)先假设存在,并设出直线
的方程;(2)先假设存在,并设出直线![]() 的方程,联立直线与椭圆,结合韦达定理得到
的方程,联立直线与椭圆,结合韦达定理得到![]() 中点的坐标,进而表示出点
中点的坐标,进而表示出点![]() 的坐标,再根据点
的坐标,再根据点![]() 在椭圆上,可求出直线
在椭圆上,可求出直线![]() 的方程.
的方程.
试题解析:(1)设动点![]() ,
,
![]() 动点
动点![]() 到定点
到定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离之比是常数
的距离之比是常数![]() ,
,
![]() 由题意,得
由题意,得 ,
,
化简整理得![]() 的方程为
的方程为![]() .
.
![]() 轨迹
轨迹![]() 的方程为
的方程为![]() . ...(3分)
. ...(3分)
(2)假设存在![]() 满足条件.依题意设直线
满足条件.依题意设直线![]() 为
为![]() ,
,
联立 ,消去
,消去![]() ,得
,得![]() ,
,
令![]() ,
,![]() ,
,
则![]() ,
,![]() ,...(7分)
,...(7分)
![]() 的中点
的中点![]() 的坐标为
的坐标为![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,解得
,解得![]() ,即
,即![]() . ...(9分)
. ...(9分)
![]() 、
、![]() 关于
关于![]() 点对称,
点对称,![]() ,
,![]() ,
,
解得![]() ,
,![]() ,即
,即![]() . ...(11分)
. ...(11分)
![]() 点
点![]() 在椭圆上,
在椭圆上, ,
,
解得![]() ,
,![]() ,
,![]() ,
,
![]() 的方程为
的方程为![]() 或
或![]() . ...(13分)
. ...(13分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来我国电子商务行业迎来篷勃发展的新机遇,2016年双11期间,某购物平台的销售业绩高达一千多亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(Ⅰ)请完成如下列联表;
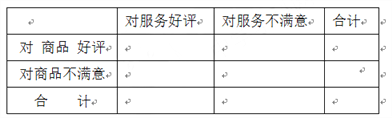
(Ⅱ)是否可以在犯错误的概率不超过0.1%的前提下,认为商品好评与服务好评有关?
(Ⅲ)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.

(
 ,其中
,其中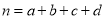 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)证明:函数
 是偶函数;
是偶函数;(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图像(草图),并写出函数的值域;
(3)在同一坐标系中画出直线
 ,观察图像写出不等式
,观察图像写出不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京时间3月15日下午,谷歌围棋人工智能
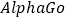 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,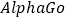 获得本场比赛胜利,最终人机大战总比分定格在
获得本场比赛胜利,最终人机大战总比分定格在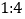 .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.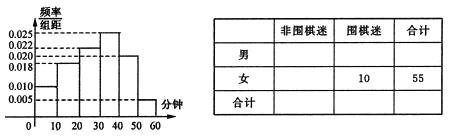
(1)根据已知条件完成如图列联表,并据此资料判断你是否有
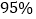 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为
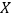 .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求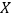 的分布列,期望
的分布列,期望 和方差
和方差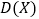 .
.附:
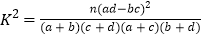 ,其中
,其中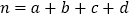 .
.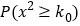
0.05
0.010
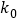
3.74
6.63
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1,求函数f(x)的解析式.
(2)已知x+y=12,xy=9且x<y,求
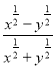 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为
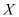 ,求
,求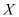 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
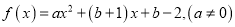 ,若存在实数
,若存在实数 ,使
,使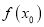 =
=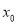 成立,则称
成立,则称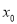 为
为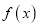 的不动点.
的不动点.⑴当
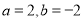 时,求
时,求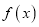 的不动点;
的不动点;(2)当
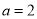 时,函数
时,函数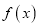 在
在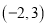 内有两个不同的不动点,求实数
内有两个不同的不动点,求实数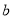 的取值范围;
的取值范围;(3)若对于任意实数
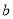 ,函数
,函数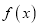 恒有两个不相同的不动点,求实数
恒有两个不相同的不动点,求实数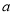 的取值范围.
的取值范围.
相关试题

