【题目】(1)已知函数f(x)(x∈R)是奇函数,且当x>0时,f(x)=2x-1,求函数f(x)的解析式.
(2)已知x+y=12,xy=9且x<y,求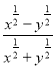 的值.
的值.
参考答案:
【答案】(1)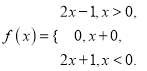 ;(2)
;(2)![]() .
.
【解析】试题分析: 利用函数的奇偶性求函数的解析式是函数的奇偶性的应用之一,给出函数在x>0的解析式,利用当x<0时,-x>0,借助f(x)=-f(-x)就可以求出x<0时的解析式;指数幂运算要严格按照幂运算定义和法则运算,法则包括同底数幂相乘,底数不变,指数相加;同底数幂相除,底数不变指数相减;幂的乘方,底数不变指数相乘;积的乘方等于把积中每个因数乘方,再把所得的幂相乘;本题就是初中的分母有理化,将原式化简后代入求值.
试题解析:
(1)当x<0,-x>0,∴f(-x)=2(-x)-1=-2x-1.
又∵f(x)是奇函数,∴f(-x)=-f(x),
∴f(x)=2x+1.又f(x)(x∈R)是奇函数,
∴f(-0)=-f(0),即f(0)=0.
∴所求函数的解析式为f(x)= ,
,
(2)解 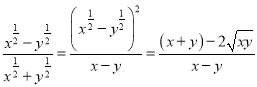 .①
.①
∵x+y=12,xy=9,②
∴(x-y)2=(x+y)2-4xy=122-4×9=108.
又∵x<y,∴x-y=-6![]() .③
.③
将②③代入①,得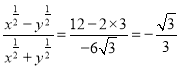 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)证明:函数
 是偶函数;
是偶函数;(2)利用绝对值及分段函数知识,将函数解析式写成分段函数的形式,然后画出函数图像(草图),并写出函数的值域;
(3)在同一坐标系中画出直线
 ,观察图像写出不等式
,观察图像写出不等式 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京时间3月15日下午,谷歌围棋人工智能
 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量, 获得本场比赛胜利,最终人机大战总比分定格在
获得本场比赛胜利,最终人机大战总比分定格在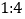 .人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.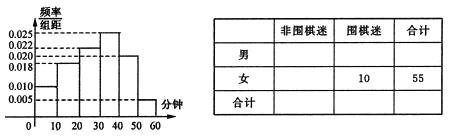
(1)根据已知条件完成如图列联表,并据此资料判断你是否有
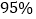 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?(2)将上述调查所得到的频率视为概率.现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记所抽取的3名学生中的“围棋迷”人数为
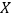 .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求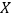 的分布列,期望
的分布列,期望 和方差
和方差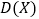 .
.附:
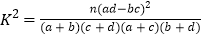 ,其中
,其中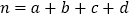 .
.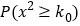
0.05
0.010
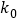
3.74
6.63
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,动点
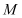 到定点
到定点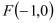 的距离和它到直线
的距离和它到直线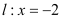 的距离
的距离之比是常数
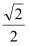 ,记动点
,记动点 的轨迹为
的轨迹为 .
.(1)求轨迹
 的方程;
的方程;(2)过点
 且不与
且不与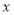 轴重合的直线
轴重合的直线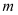 ,与轨迹
,与轨迹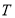 交于
交于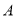 ,
,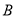 两点,线段
两点,线段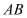 的垂直平分线与
的垂直平分线与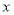 轴交于点
轴交于点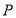 ,与轨迹
,与轨迹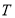 是否存在点
是否存在点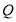 ,使得四边形
,使得四边形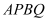 为菱形?若存在,请求出直线
为菱形?若存在,请求出直线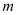 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为
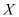 ,求
,求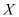 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
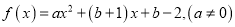 ,若存在实数
,若存在实数 ,使
,使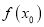 =
=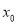 成立,则称
成立,则称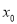 为
为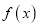 的不动点.
的不动点.⑴当
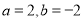 时,求
时,求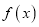 的不动点;
的不动点;(2)当
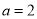 时,函数
时,函数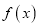 在
在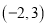 内有两个不同的不动点,求实数
内有两个不同的不动点,求实数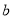 的取值范围;
的取值范围;(3)若对于任意实数
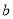 ,函数
,函数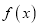 恒有两个不相同的不动点,求实数
恒有两个不相同的不动点,求实数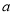 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
相关试题

