【题目】定义在非零实数集上的函数![]() 满足:
满足: ![]() ,且
,且![]() 在区间
在区间![]() 上为递增函数.
上为递增函数.
(1)求![]() 、
、![]() 的值;
的值;
(2)求证: ![]() 是偶函数;
是偶函数;
(3)解不等式![]() .
.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:本题为抽象函数问题,解决抽象函数的基本方法有两种:一是赋值法,二是“打回原型”,本题第一步采用赋值法,先给x,y赋值1,求出f(1),再给x,y赋值-1,求出f(-1);最后给y赋值-1,判断函数奇偶性,就是寻求f(-x)与f(x)的关系,给y赋值-1,判断出函数的奇偶性;再根据函数的奇偶性,得出函数图像的对称性,利用已知所提供的函数的单调性,借助f(-1)=f(1)=0,画出函数的图像,根据函数的奇偶性和单调性转化不等式,解不等式.
试题解析:
⑴令![]() 则
则![]() 即
即![]()
令![]() 则
则![]() 即
即![]()
⑵令![]() 则
则![]() 即
即![]()
![]() 为偶函数
为偶函数
⑶由题意可知![]() 的大致图象为
的大致图象为

![]() 原不等式等价于
原不等式等价于![]()
即![]() 且
且![]()
![]() 不等式的解集为
不等式的解集为![]()
【点精】本题为抽象函数问题,解决抽象函数的基本方法有两种:一是赋值法,二是“打回原型”,赋值法是最常用的解题方法,巧妙的赋值可求出函数的特值,也可以判断抽象函数的奇偶性,也可以证明函数的单调性,借助函数的奇偶性和单调性以及特殊点特殊值可以模拟出函数的图象,在此基础上可以解不等式或解决其它函数问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为
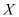 ,求
,求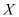 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
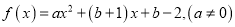 ,若存在实数
,若存在实数 ,使
,使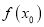 =
=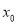 成立,则称
成立,则称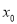 为
为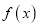 的不动点.
的不动点.⑴当
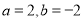 时,求
时,求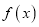 的不动点;
的不动点;(2)当
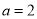 时,函数
时,函数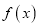 在
在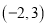 内有两个不同的不动点,求实数
内有两个不同的不动点,求实数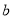 的取值范围;
的取值范围;(3)若对于任意实数
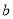 ,函数
,函数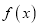 恒有两个不相同的不动点,求实数
恒有两个不相同的不动点,求实数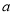 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
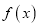 的定义域为D,若函数
的定义域为D,若函数 满足条件:存在
满足条件:存在 ,使
,使 在
在 上的值域为
上的值域为 ,则称
,则称 为“倍缩函数”,若函数
为“倍缩函数”,若函数 为“倍缩函数”,则实数
为“倍缩函数”,则实数 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6位选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图.为了增加结果的神秘感,主持人暂时没有公布甲、乙两班最后一位选手的成绩.
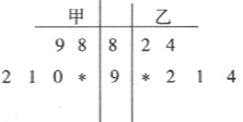
(Ⅰ)求乙班总分超过甲班的概率;
(Ⅱ)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.请你从平均分和方差的角度来分析两个班的选手的情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
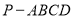 中,底面
中,底面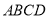 为直角梯形,
为直角梯形, ,
,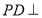 底面
底面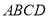 ,
, ,
,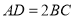 ,
,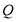 为
为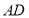 的中点,
的中点, 为棱
为棱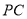 的中点.
的中点.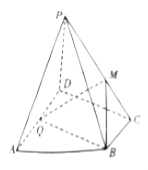
(I)证明:
 平面
平面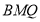 ;
;(II)已知
 ,求
,求 点到平面
点到平面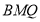 的距离.
的距离.
相关试题

