【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出![]() 次成功交易,并对其评价进行统计爱,商品和服务评价的
次成功交易,并对其评价进行统计爱,商品和服务评价的![]() 列联表如下表:
列联表如下表:
对服务好评 | 对服务不满意 | 合计 | |
对商品好评 |
|
|
|
对商品不满意 |
|
|
|
合计 |
|
|
|
(1)是否可以在犯错误概率不超过![]() 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的![]() 次购物中,设对商品和服务全好评的次数为随机变量
次购物中,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(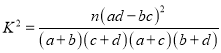 ,其中
,其中![]() )
)
参考答案:
【答案】(1)可以(2)见解析
【解析】试题分析:(1)由已知列出关于商品和服务评价的2×2列联表,代入公式求得k2的值,对应数表得答案;
(2)每次购物时,对商品和服务全好评的概率为0.4,且X的取值可以是0,1,2,3,X~B(3,0.4).求出相应的概率,可得对商品和服务全好评的次数X的分布列(概率用组合数算式表示);利用二项分布的数学期望和方差求X的数学期望.
试题解析:
解:(1)![]() ,可以在犯错误概率不超过
,可以在犯错误概率不超过![]() 的前提下,认为商品好评与服务好评有关.
的前提下,认为商品好评与服务好评有关.
(2)由题意![]() 的取值可以是
的取值可以是![]() .每次购物时,对商品和服务都好评的概率为
.每次购物时,对商品和服务都好评的概率为![]()
所以![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AC=AD,AH⊥CD于H,BD交AH于P,且PC⊥BC

(1)求证:A,B,C,P四点共圆;
(2)若∠CAD= ,AB=1,求四边形ABCP的面积.
,AB=1,求四边形ABCP的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线l的参数方程为:
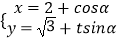 (t为参数,其中0<α<
(t为参数,其中0<α<  ),椭圆M的参数方程为
),椭圆M的参数方程为 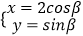 (β为参数),圆C的标准方程为(x﹣1)2+y2=1.
(β为参数),圆C的标准方程为(x﹣1)2+y2=1.
(1)写出椭圆M的普通方程;
(2)若直线l为圆C的切线,且交椭圆M于A,B两点,求弦AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣2|+|x﹣a|.
(1)当a=2时,求不等式f(x)≥4的解集;
(2)不等式f(x)<4的解集中的整数有且仅有1,2,3,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知X和Y是两个分类变量,由公式K2=
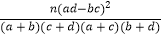 算出K2的观测值k约为7.822根据下面的临界值表可推断( )
算出K2的观测值k约为7.822根据下面的临界值表可推断( ) P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
A.推断“分类变量X和Y没有关系”犯错误的概率上界为0.010
B.推断“分类变量X和Y有关系”犯错误的概率上界为0.010
C.有至少99%的把握认为分类变量X和Y没有关系
D.有至多99%的把握认为分类变量X和Y有关系 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x2﹣4x+a,g(x)=logax(a>0且a≠1).
(1)若函数f(x)在[﹣1,2m]上不具有单调性,求实数m的取值范围;
(2)若f(1)=g(1).
(ⅰ)求实数a的值;
(ⅱ)设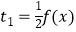 ,t2=g(x),
,t2=g(x), 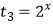 ,当x∈(0,1)时,试比较t1 , t2 , t3的大小.
,当x∈(0,1)时,试比较t1 , t2 , t3的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域.
相关试题

