【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域.
参考答案:
【答案】
(1)
解:∵f(x)=log2(x+1),g(x)=log2(3x+1),g(x)≥f(x),
∴3x+1≥x+1>0,
∴x≥0.
即使g(x)≥f(x)成立的x的取值范围为[0,+∞)
(2)
解:∵y=g(x)﹣f(x)
=log2(3x+1)﹣log2(x+1)
=log2 ![]() (x≥0).
(x≥0).
令h(x)= ![]() =3﹣
=3﹣ ![]() ,
,
则h(x)为[0,+∞)上的增函数,
∴1≤h(x)<3,
故y=g(x)﹣f(x)∈[0,log23],
即函数y=g(x)﹣f(x)的值域为[0,log23]
【解析】(1)利用对数函数y=log2x的单调性即可求得g(x)≥f(x)成立的x的取值范围;(2)分析函数y=g(x)﹣f(x)的单调性,结合x∈[0,+∞)可得函数y=g(x)﹣f(x)的值域.
【考点精析】利用对数函数的定义域和对数函数的单调区间对题目进行判断即可得到答案,需要熟知对数函数的定义域范围:(0,+∞);a变化对图象的影响:在第一象限内,a越大图象越靠低;在第四象限内,a越大图象越靠高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来我国电子商务行业迎来蓬勃发展的新机遇相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出
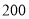 次成功交易,并对其评价进行统计爱,商品和服务评价的
次成功交易,并对其评价进行统计爱,商品和服务评价的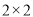 列联表如下表:
列联表如下表:对服务好评
对服务不满意
合计
对商品好评
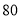
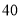
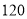
对商品不满意
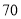
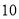
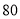
合计
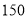
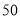
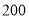
(1)是否可以在犯错误概率不超过
 的前提下,认为商品好评与服务好评有关?
的前提下,认为商品好评与服务好评有关?(2)若将频率视为概率,某人在该购物平台上进行的
 次购物中,设对商品和服务全好评的次数为随机变量
次购物中,设对商品和服务全好评的次数为随机变量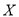 ,求
,求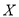 的数学期望.
的数学期望.参考数据:
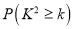
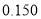
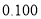
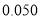
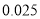
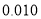
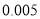

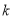
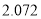

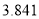

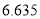
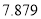
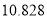
(
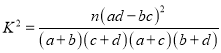 ,其中
,其中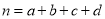 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知X和Y是两个分类变量,由公式K2=
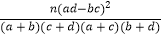 算出K2的观测值k约为7.822根据下面的临界值表可推断( )
算出K2的观测值k约为7.822根据下面的临界值表可推断( ) P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
A.推断“分类变量X和Y没有关系”犯错误的概率上界为0.010
B.推断“分类变量X和Y有关系”犯错误的概率上界为0.010
C.有至少99%的把握认为分类变量X和Y没有关系
D.有至多99%的把握认为分类变量X和Y有关系 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x2﹣4x+a,g(x)=logax(a>0且a≠1).
(1)若函数f(x)在[﹣1,2m]上不具有单调性,求实数m的取值范围;
(2)若f(1)=g(1).
(ⅰ)求实数a的值;
(ⅱ)设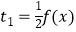 ,t2=g(x),
,t2=g(x), 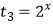 ,当x∈(0,1)时,试比较t1 , t2 , t3的大小.
,当x∈(0,1)时,试比较t1 , t2 , t3的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga
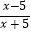 ,(a>0且a≠1).
,(a>0且a≠1).
(1)判断f(x)的奇偶性,并加以证明;
(2)是否存在实数m使得f(x+2)+f(m﹣x)为常数?若存在,求出m的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一种计算装置,有一数据入口A和一个运算出口B,按照某种运算程序:①当从A口输入自然数1时,从B口得到
 ,记为
,记为 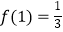 ;②当从A口输入自然数n(n≥2)时,在B口得到的结果f(n)是前一个结果f(n﹣1)的
;②当从A口输入自然数n(n≥2)时,在B口得到的结果f(n)是前一个结果f(n﹣1)的 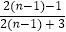 倍. (Ⅰ)当从A口分别输入自然数2,3,4时,从B口分别得到什么数?
倍. (Ⅰ)当从A口分别输入自然数2,3,4时,从B口分别得到什么数?
(Ⅱ)根据(Ⅰ)试猜想f(n)的关系式,并用数学归纳法证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( )
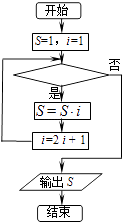
A.i≤31?
B.i≤63?
C.i≥63?
D.i≤127?
相关试题

