【题目】下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量![]() 的性质
的性质![]() ,类比得到复数
,类比得到复数![]() 的性质
的性质![]() ;
;
③方程![]() 有两个不同实数根的条件是
有两个不同实数根的条件是![]() 可以类比得到:方程
可以类比得到:方程![]() 有两个不同复数根的条件是
有两个不同复数根的条件是![]() ;
;
④由向量加法的几何意义可以类比得到复数加法的几何意义,其中类比错误的是__________.
参考答案:
【答案】②③
【解析】分析:①由两者运算规则判断;②由定义判断;③可由两者运算特征进行判断;④由两者加法的几何意义判断.
详解:①复数的加减法运算可以类比多项式的加减法运算,两者用的都是合并同类项的规则,可以类比;
②由向量![]() 的性质
的性质![]() ,类比得到复数
,类比得到复数![]() 的性质
的性质![]() ,两者属性不同,一个是数,一个是既有大小又有方向的量,不具有类比性,故错误;
,两者属性不同,一个是数,一个是既有大小又有方向的量,不具有类比性,故错误;
③方程![]() 有两个不同实数根的条件是
有两个不同实数根的条件是![]() 可以类比得到:方程
可以类比得到:方程![]() 有两个不同复数根的条件是
有两个不同复数根的条件是![]() ,数的概念的推广后,原有的概念在新的领域里是不是成立属于知识应用的推广,不是类比,故错误;
,数的概念的推广后,原有的概念在新的领域里是不是成立属于知识应用的推广,不是类比,故错误;
④由向量加法的几何意义可以类比得到复数加法的几何意义,由两者的几何意义知,此类比正确;
综上,②③是错误的,故答案为②③.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ae2x﹣be﹣2x﹣cx(a,b,c∈R)的导函数f′(x)为偶函数,且曲线y=f(x)在点(0,f(0))处的切线的斜率为4﹣c.
(1)确定a,b的值;
(2)若c=3,判断f(x)的单调性;
(3)若f(x)有极值,求c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设椭圆
 (a>b>0)的左、右焦点分别为F1 , F2 , 点D在椭圆上.DF1⊥F1F2 ,
(a>b>0)的左、右焦点分别为F1 , F2 , 点D在椭圆上.DF1⊥F1F2 , 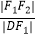 =2
=2  ,△DF1F2的面积为
,△DF1F2的面积为  .
. 
(1)求椭圆的标准方程;
(2)设圆心在y轴上的圆与椭圆在x轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a1=1,an+1=
 +b(n∈N*)
+b(n∈N*)
(1)若b=1,求a2 , a3及数列{an}的通项公式;
(2)若b=﹣1,问:是否存在实数c使得a2n<c<a2n+1对所有的n∈N*成立,证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
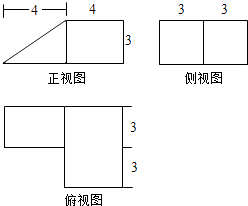
A.90cm2
B.129cm2
C.132cm2
D.138cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】2002年北京国际数学家大会会标,是以中国古代数学家赵爽的弦图为基础而设计的,弦图用四个全等的直角三角形与一个小正方形拼成的一个大正方形
 如图
如图 ,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为
,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为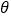 ,则
,则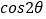 等于
等于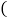

A.
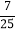 B.
B.  C.
C. 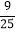 D.
D. 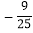
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,的部分图象如图所示.
,的部分图象如图所示.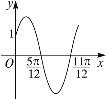
(Ⅰ)求函数
 的解析式;
的解析式;(Ⅱ)求函数
 的单调递增区间.
的单调递增区间.
相关试题

