【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,
上,![]() 为坐标原点,
为坐标原点,![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)圆![]() 与抛物线
与抛物线![]() 顺次交于
顺次交于![]() 四点,
四点,![]() 所在的直线
所在的直线![]() 过焦点
过焦点![]() ,线段
,线段![]() 是圆
是圆![]() 的直径,
的直径,![]() ,求直线
,求直线![]() 的方程..
的方程..
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ..
..
【解析】
(1) 将![]() 代入抛物线
代入抛物线![]() 的方程,得
的方程,得![]() ,结合抛物线定义可得
,结合抛物线定义可得![]() 值;
值;
(2)由题设知![]() 与坐标轴不垂直,可设
与坐标轴不垂直,可设![]() ,代入
,代入![]() ,得
,得![]() .利用韦达定理可得
.利用韦达定理可得![]() 的中点为
的中点为![]() 及
及![]() ,
,![]() 的方程为
的方程为![]() ,代入
,代入![]() ,并整理得
,并整理得![]() .利用韦达定理可得
.利用韦达定理可得![]() 的中点为
的中点为![]() 及
及![]() ,结合勾股定理即可得到结果.
,结合勾股定理即可得到结果.
解:(1)将![]() 代入抛物线
代入抛物线![]() 的方程,得
的方程,得![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,整理得
,整理得![]() ,
,
解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,满足
,满足![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() .
.
(2)由题设知![]() 与坐标轴不垂直,可设
与坐标轴不垂直,可设![]() ,代入
,代入![]() ,得
,得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
故![]() 的中点为
的中点为![]() ,
,![]() .
.
又因为![]() ,所以
,所以![]() 的斜率为
的斜率为![]() ,
,![]() 过
过![]() 的中点
的中点![]() ,
,
所以![]() 的方程为
的方程为![]() ,即
,即![]() .
.
将上式代入![]() ,并整理得
,并整理得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,故
,故![]() 的中点为
的中点为![]() ,
,![]() .
.
因为![]() 是直径,所以
是直径,所以![]() 垂直平分
垂直平分![]() ,
,
所以![]() 四点在同一个圆上等价于
四点在同一个圆上等价于![]() ,
,
所以![]() ,
,
即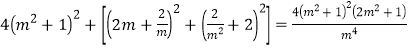 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过椭圆
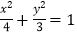 的右焦点F作两条相互垂直的直线分别交椭圆于A,B,C,D四点,则
的右焦点F作两条相互垂直的直线分别交椭圆于A,B,C,D四点,则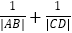 的值为( )
的值为( )A.
 B.
B.  C. 1 D.
C. 1 D. 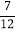
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
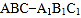 中,
中,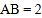 ,
, ,
,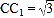 ,
,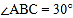 ,
,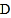 为
为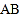 的中点.
的中点.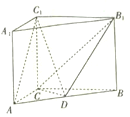
(1)证明:
 平面
平面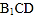 ;
;(2)求直线
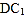 与平面
与平面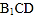 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形
 中,
中, 分别为内角
分别为内角 所对的边,且满足
所对的边,且满足 .
.(1)求角
 的大小;
的大小;(2)若
 ,且
,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知斜率为
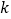 的直线
的直线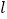 与椭圆
与椭圆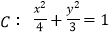 交于
交于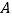 ,
,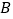 两点,线段
两点,线段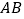 的中点为
的中点为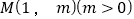 .
.(1)证明:
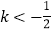 ;
;(2)设
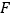 为
为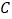 的右焦点,
的右焦点,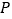 为
为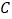 上一点,且
上一点,且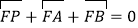 .证明:
.证明: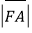 ,
, ,
,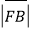 成等差数列,并求该数列的公差.
成等差数列,并求该数列的公差. -
科目: 来源: 题型:
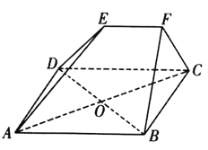
查看答案和解析>>【题目】如图,在多面体
 中,四边形
中,四边形 是边长为
是边长为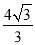 的菱形,
的菱形, ,
, 与
与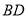 交于点
交于点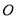 ,平面
,平面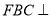 平面
平面 ,
,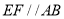 ,
,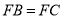 ,
,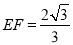 .
.
(1)求证:
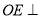 平面
平面 ;
;(2)若
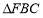 为等边三角形,点
为等边三角形,点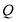 为
为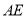 的中点,求二面角
的中点,求二面角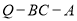 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
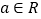 ,函数
,函数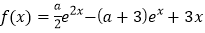 .
. (1)讨论
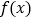 的单调性;
的单调性;(2)若
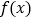 有两个零点,求实数
有两个零点,求实数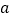 的取值范围.
的取值范围.
相关试题

