【题目】在锐角三角形![]() 中,
中,![]() 分别为内角
分别为内角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】解:(Ⅰ)因为![]() ,
,
所以![]() , ……………………………………………… 2分
, ……………………………………………… 2分
因为![]() ,所以
,所以![]() . …………………………………………………3分
. …………………………………………………3分
又![]() 为锐角,则
为锐角,则![]() . …………………………………………… 5分
. …………………………………………… 5分
(Ⅱ)由(Ⅰ)可知,![]() .因为
.因为![]() ,
,
根据余弦定理,得![]() ,………………………………………7分
,………………………………………7分
整理,得![]() .
.
由已知![]() ,则
,则![]() .
.
又![]() ,可得
,可得![]() ,
,![]() . ……………………………………… 9分
. ……………………………………… 9分
于是![]() , ………………………… 11分
, ………………………… 11分
所以![]() . …………… 13分
. …………… 13分
【解析】试题分析:(1)由正弦定理可得![]() ,即
,即![]() ,则角
,则角![]() 可求;
可求;
(2))由(1)知,![]() ,由余弦定理可得
,由余弦定理可得![]() ,进而求得
,进而求得![]() 则
则![]() 的值可求
的值可求
试题解析:(1)因为![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以![]() ,又
,又![]() 为锐角,则
为锐角,则![]() .
.
(2)由(1)知,![]() ,因为
,因为![]() ,根据余弦定理得:
,根据余弦定理得:![]() ,整理,得
,整理,得![]() ,由已知
,由已知![]() ,则
,则![]() ,又
,又![]() ,可得
,可得![]() ,于是
,于是![]() ,
,
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 过点
过点 ,过右焦点且垂直于
,过右焦点且垂直于 轴的直线截椭圆所得弦长是1.
轴的直线截椭圆所得弦长是1.(1)求椭圆
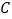 的标准方程;
的标准方程;(2)设点
 分别是椭圆
分别是椭圆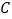 的左,右顶点,过点
的左,右顶点,过点 的直线
的直线 与椭圆交于
与椭圆交于 两点(
两点( 与
与 不重合),证明:直线
不重合),证明:直线 和直线
和直线 交点的横坐标为定值.
交点的横坐标为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)当
 时,证明:对任意的
时,证明:对任意的 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
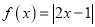 .
.(Ⅰ)求不等式
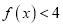 ;
;(Ⅱ)若函数
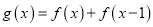 的最小值为
的最小值为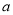 ,且
,且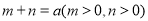 ,求
,求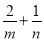 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
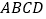 是边长为
是边长为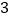 的正方形,
的正方形,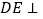 平面
平面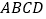 ,
,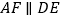 ,
,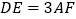 ,
,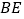 与平面
与平面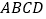 所成角为
所成角为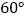 .
.(Ⅰ)求证:
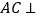 平面
平面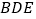 .
.(Ⅱ)求二面角
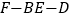 的余弦值.
的余弦值.(Ⅲ)设点
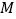 是线段
是线段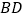 上一个动点,试确定点
上一个动点,试确定点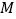 的位置,使得
的位置,使得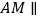 平面
平面 ,并证明你的结论.
,并证明你的结论.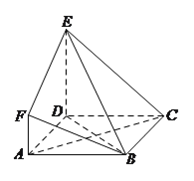
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
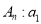 ,
, 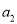 ,
, 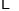 ,
, 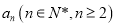 满足
满足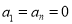 ,且当
,且当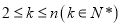 时,
时, 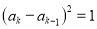 ,令
,令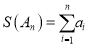 .
.(Ⅰ)写出
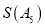 的所有可能的值.
的所有可能的值.(Ⅱ)求
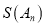 的最大值.
的最大值.(Ⅲ)是否存在数列
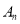 ,使得
,使得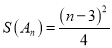 ?若存在,求出数列
?若存在,求出数列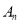 ;若不存在,说明理由.
;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
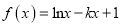 .
.(1)求
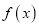 的单调区间;
的单调区间;(2)若
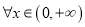 ,都有
,都有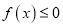 ,求实数
,求实数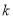 的取值范围;
的取值范围;(3)证明:
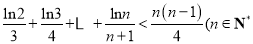 且
且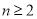 ).
).
相关试题

