【题目】已知斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)证明:![]() ;
;
(2)设![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,且
上一点,且![]() .证明:
.证明:![]() ,
,![]() ,
,![]() 成等差数列,并求该数列的公差.
成等差数列,并求该数列的公差.
参考答案:
【答案】(1)![]()
(2)![]() 或
或![]()
【解析】分析:(1)设而不求,利用点差法进行证明。
(2)解出m,进而求出点P的坐标,得到![]() ,再由两点间距离公式表示出
,再由两点间距离公式表示出![]() ,得到直
,得到直![]() 的方程,联立直线与椭圆方程由韦达定理进行求解。
的方程,联立直线与椭圆方程由韦达定理进行求解。
详解:(1)设![]() ,则
,则![]() .
.
两式相减,并由![]() 得
得
![]() .
.
由题设知![]() ,于是
,于是
![]() .①
.①
由题设得![]() ,故
,故![]() .
.
(2)由题意得![]() ,设
,设![]() ,则
,则
![]() .
.
由(1)及题设得![]() .
.
又点P在C上,所以![]() ,从而
,从而![]() ,
,![]() .
.
于是
![]() .
.
同理![]() .
.
所以![]() .
.
故![]() ,即
,即![]() 成等差数列.
成等差数列.
设该数列的公差为d,则
![]() .②
.②
将![]() 代入①得
代入①得![]() .
.
所以l的方程为![]() ,代入C的方程,并整理得
,代入C的方程,并整理得![]() .
.
故![]() ,代入②解得
,代入②解得![]() .
.
所以该数列的公差为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
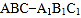 中,
中,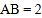 ,
, ,
,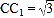 ,
,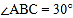 ,
,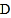 为
为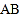 的中点.
的中点.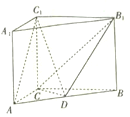
(1)证明:
 平面
平面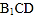 ;
;(2)求直线
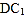 与平面
与平面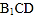 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形
 中,
中, 分别为内角
分别为内角 所对的边,且满足
所对的边,且满足 .
.(1)求角
 的大小;
的大小;(2)若
 ,且
,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为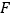 ,点
,点 在抛物线
在抛物线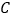 上,
上,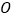 为坐标原点,
为坐标原点,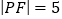 ,且
,且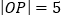 .
.(1)求抛物线
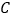 的方程;
的方程;(2)圆
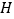 与抛物线
与抛物线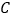 顺次交于
顺次交于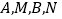 四点,
四点,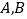 所在的直线
所在的直线 过焦点
过焦点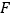 ,线段
,线段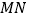 是圆
是圆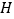 的直径,
的直径,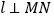 ,求直线
,求直线 的方程..
的方程.. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在多面体
 中,四边形
中,四边形 是边长为
是边长为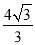 的菱形,
的菱形, ,
, 与
与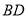 交于点
交于点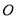 ,平面
,平面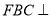 平面
平面 ,
,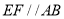 ,
,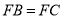 ,
,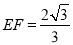 .
.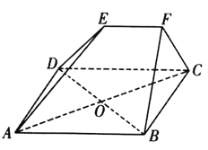
(1)求证:
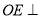 平面
平面 ;
;(2)若
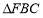 为等边三角形,点
为等边三角形,点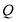 为
为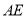 的中点,求二面角
的中点,求二面角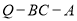 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
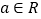 ,函数
,函数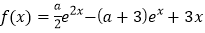 .
. (1)讨论
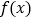 的单调性;
的单调性;(2)若
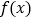 有两个零点,求实数
有两个零点,求实数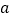 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校有教师400人,对他们进行年龄状况和学历的调查,其结果如下:
学历
35岁以下
35-55岁
55岁及以上
本科
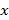
60
40
硕士
80
40
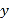
(1)若随机抽取一人,年龄是35岁以下的概率为
 ,求
,求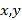 ;
;(2)在35-55岁年龄段的教师中,按学历状况用分层抽样的方法,抽取一个样本容量为5的样本,然后在这5名教师中任选2人,求两人中至多有1人的学历为本科的概率.
相关试题

