【题目】某校为选拔参加“央视猜灯谜大赛”的队员,在校内组织猜灯谜竞赛.规定:第一阶段知识测试成绩不小于160分的学生进入第二阶段比赛.现有200名学生参加知识测试,并将所有测试成绩绘制成如下所示的频率分布直方图.
(Ⅰ)估算这200名学生测试成绩的中位数,并求进入第二阶段比赛的学生人数;
(Ⅱ)将进入第二阶段的学生分成若干队进行比赛.现甲、乙两队在比赛中均已获得120分,进入最后抢答阶段.抢答规则:抢到的队每次需猜3条谜语,猜对1条得20分,猜错1条扣20分.根据经验,甲队猜对每条谜语的概率均为 ![]() ,乙队猜对前两条的概率均为
,乙队猜对前两条的概率均为 ![]() ,猜对第3条的概率为
,猜对第3条的概率为 ![]() .若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
.若这两队抢到答题的机会均等,您做为场外观众想支持这两队中的优胜队,会把支持票投给哪队?
参考答案:
【答案】解:(Ⅰ)设测试成绩的中位数为x,由频率分布直方图得,
(0.0015+0.019)×20+(x﹣140)×0.025=0.5,
解得:x=143.6.
∴测试成绩中位数为143.6.
进入第二阶段的学生人数为200×(0.003+0.0015)×20=18人.
(Ⅱ)设最后抢答阶段甲、乙两队猜对灯谜的条数分别为ξ、η,
则ξ~B(3, ![]() ),
),
∴E(ξ)= ![]() .
.
∴最后抢答阶段甲队得分的期望为[ ![]() ]×20=30,
]×20=30,
∵P(η=0)= ![]() ,
,
P(η=1)= ![]() ,
,
P(η=2)= ![]() ,
,
P(η=3)= ![]() ,
,
∴Eη= ![]() .
.
∴最后抢答阶段乙队得分的期望为[ ![]() ]×20=24.
]×20=24.
∴120+30>120+24,
∴支持票投给甲队
【解析】(Ⅰ)设测试成绩的中位数为x,由频率分布直方图中x两侧的矩形的面积相等列式求得x值,则中位数可求,再由200×(0.003+0.0015)×20求得进入第二阶段的学生人数;(Ⅱ)设最后抢答阶段甲、乙两队猜对灯谜的条数分别为ξ、η,则ξ服从B(3, ![]() )分布,由此求得Eξ,进一步求得最后抢答阶段甲队得分的期望,然后求出Eη,再求出最后抢答阶段乙队得分的期望,比较期望后得答案.
)分布,由此求得Eξ,进一步求得最后抢答阶段甲队得分的期望,然后求出Eη,再求出最后抢答阶段乙队得分的期望,比较期望后得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.则函数y=f(x)( )
A.有极小值,无极大值
B.有极大值,无极小值
C.既有极小值又有极大值
D.既无极小值又无极大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】若数列{an}前n项和为Sn , a1=a2=2,且满足Sn+Sn+1+Sn+2=3n2+6n+5,则S47等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数列{an}前n项和为Sn , a1=a2=2,且满足Sn+Sn+1+Sn+2=3n2+6n+5,则S47等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角 ,
, ,
,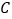 所对的边分别为
所对的边分别为 ,
,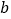 ,
, ,且
,且 ,则下列结论正确的是( )
,则下列结论正确的是( )A.
 B.
B. 是钝角三角形
是钝角三角形C.
 的最大内角是最小内角的
的最大内角是最小内角的 倍D.若
倍D.若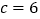 ,则
,则 外接圆半径为
外接圆半径为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
(Ⅰ)求证:BC⊥平面ACFE;
(Ⅱ)点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
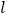 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,以
为极点,以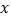 轴正半轴为极轴,建立极坐标系,圆
轴正半轴为极轴,建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.(1)求直线
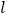 的普通方程和圆
的普通方程和圆 的直角坐标方程;
的直角坐标方程;(2)若点
 是直线
是直线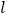 上的动点,过
上的动点,过 作直线与圆
作直线与圆 相切,切点分别为
相切,切点分别为 、
、 ,若使四边形
,若使四边形 的面积最小,求此时点
的面积最小,求此时点 的坐标.
的坐标.
相关试题

