【题目】已知函数f(x)=( ![]() +a)x,a∈R
+a)x,a∈R
(1)求函数的定义域
(2)是否存在实数a,使得f(x)为偶函数.
参考答案:
【答案】
(1)解:由题意,2x﹣1≠0,∴x≠0,
∴函数的定义域为{x|x≠0}
(2)解:设f(x)为偶函数,则f(﹣x)=f(x),
即( ![]() +a)x=(
+a)x=( ![]() +a)x,
+a)x,
∴2a= ![]() ﹣
﹣ ![]() =1,
=1,
∴ ![]()
【解析】(1)利用分母不为0,可得函数的定义域;(2)利用f(﹣x)=f(x),求出a.
【考点精析】认真审题,首先需要了解函数的定义域及其求法(求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零),还要掌握函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇)的相关知识才是答题的关键.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零),还要掌握函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
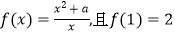 .
.
(1)判断并证明函数f(x)在其定义域上的奇偶性;
(2)证明函数f(x)在(1,+∞)上是增函数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出假设H:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算的K2≈3.918,经查临界值表知P(K2≥3.841)≈0.05.则下列表述中正确的是( )
A.有95℅的把握认为“这种血清能起到预防感冒的作用”
B.若有人未使用该血清,那么他一年中有95℅的可能性得感冒
C.这种血清预防感冒的有效率为95℅
D.这种血清预防感冒的有效率为5℅ -
科目: 来源: 题型:
查看答案和解析>>【题目】分类变量X和Y的列联表如下:
y1
y2
总计
x1
a
b
a+b
x2
c
d
c+d
总计
a+c
b+d
a+b+c+d
则下列说法中正确的是( )
A.ad-bc越小,说明X与Y关系越弱
B.ad-bc越大,说明X与Y关系越强
C.(ad-bc)2越大,说明X与Y关系越强
D.(ad-bc)2越接近于0,说明X与Y关系越强 -
科目: 来源: 题型:
查看答案和解析>>【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下2×2列联表:
喜欢数学课
不喜欢数学课
合计
男
30
60
90
女
20
90
110
合计
50
150
200
经计算K2≈6.06,根据独立性检验的基本思想,约有(填百分数)的把握认为“性别与喜欢数学课之间有关系”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
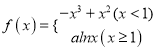
求
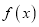 在区间
在区间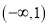 上的极小值和极大值点。
上的极小值和极大值点。求
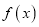 在
在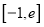 上的最大值.
上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)=
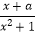 (a∈R)是奇函数,函数g(x)=
(a∈R)是奇函数,函数g(x)= 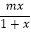 的定义域为(﹣1,+∞).
的定义域为(﹣1,+∞).
(1)求a的值;
(2)若g(x)=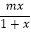 在(﹣1,+∞)上递减,根据单调性的定义求实数m的取值范围;
在(﹣1,+∞)上递减,根据单调性的定义求实数m的取值范围;
(3)在(2)的条件下,若函数h(x)=f(x)+g(x)在区间(﹣1,1)上有且仅有两个不同的零点,求实数m的取值范围.
相关试题

