搜索
【题目】已知函数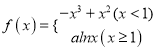
求
在区间
上的极小值和极大值点。
求
在
上的最大值.
参考答案：
【答案】(1) 
, 
极小值0， 
为极大值点.(2)当
时，最大值
，当
时，最大值为2.
【解析】试题分析：（1）当
时，求导函数，确定函数的单调性，可得
在区间
上的极小值和极大值点；（2）分两种情况
， 
讨论，分别利用导数确定函数的单调性，即可得到
在
上的极大值，与区间端点值的函数值比较即可的结果.
试题解析：（1）当
时， 
，令
，得
或
，当
变化时， 
的变化情况如下表：
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 | 极大值 |
当
时，函数
取得极小值， 
，函数
取得极大值点为
.
（2）①当
时， 
，由（1）知，函数
在
和
上单调递减，在
上单调递增， 
， 
， 
在
上的最大值为
.
②当
时， 
，当
时， 
在
上单调递增， 
，综上所述，当
时， 
在
上的最大值为
；当
时， 
在
上的最大值为
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】分类变量X和Y的列联表如下：
y1
y2
总计
x1
a
b
a+b
x2
c
d
c+d
总计
a+c
b+d
a+b+c+d
则下列说法中正确的是（ ）
A.ad－bc越小，说明X与Y关系越弱
B.ad－bc越大，说明X与Y关系越强
C.(ad－bc)2越大，说明X与Y关系越强
D.(ad－bc)2越接近于0，说明X与Y关系越强 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=（
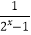+a）x，a∈R
（1）求函数的定义域
（2）是否存在实数a，使得f（x）为偶函数． -
科目： 来源： 题型：
查看答案和解析>>【题目】为考察高中生的性别与是否喜欢数学课程之间的关系，在我市某普通中学高中生中随机抽取200名学生，得到如下2×2列联表：
喜欢数学课
不喜欢数学课
合计
男
30
60
90
女
20
90
110
合计
50
150
200
经计算K2≈6.06，根据独立性检验的基本思想，约有（填百分数）的把握认为“性别与喜欢数学课之间有关系”.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知定义在R上的函数f（x）=
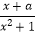（a∈R）是奇函数，函数g（x）= 
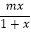的定义域为（﹣1，+∞）．
（1）求a的值；
（2）若g（x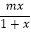）= 在（﹣1，+∞）上递减，根据单调性的定义求实数m的取值范围；
（3）在（2）的条件下，若函数h（x）=f（x）+g（x）在区间（﹣1，1）上有且仅有两个不同的零点，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
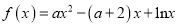.（1）当
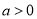时，若
在区间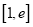
上的最小值为
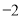，求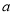
的取值范围；（2）若对任意
， 
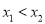，且
恒成立，求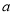
的取值范围. -
科目： 来源： 题型：
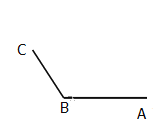
查看答案和解析>>【题目】如图所示，A ， B ， C是三个观察站，A在B的正东，两地相距6km，C在B的北偏西30°，两地相距4km，在某一时刻，A观察站发现某种信号，并知道该信号的传播速度为1km/s,4s后B ， C两个观察站同时发现这种信号，在以过A ， B两点的直线为x轴，以AB的垂直平分线为y轴建立的平面直角坐标系中，指出发出这种信号的P的坐标．
相关试题
