【题目】如图,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,将四边形
,将四边形![]() 沿
沿![]() 折起,使点
折起,使点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上.
上.
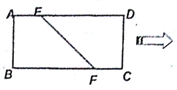
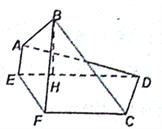
(I)求证: ![]() ;
;
(II)求点![]() 到平面
到平面![]() 的距离;
的距离;
(III)求直线![]() 与平面
与平面![]() 所成的正弦值.
所成的正弦值.
参考答案:
【答案】(1)见解析(2)2(3)![]()
【解析】试题分析:
(1)由折叠关系可得![]() 平面
平面![]() ,
, ![]() .
.
(2)利于题意结合勾股定理列方程组,求解可得点![]() 到平面
到平面![]() 的距离为2;
的距离为2;
(3)做出直线与平面所成的角,结合(1)(2)的结论可得直线![]() 与平面
与平面![]() 所成的正弦值为
所成的正弦值为![]() .
.
试题解析:
解:(1)由于![]() 平面
平面![]() ,
, ![]() ,又由于
,又由于![]() ,
, ![]() ,
,
![]() 平面
平面![]() ,
, ![]() .
.
法一:(2)设![]() ,
, ![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于
于![]() ,
,
因线段![]() ,
, ![]() 在翻折过程中长度不变,根据勾股定理:
在翻折过程中长度不变,根据勾股定理:
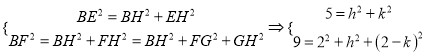 ,可解得
,可解得![]() ,
,
![]() 线段
线段![]() 长度为
长度为![]() ,即点
,即点![]() 的平面
的平面![]() 的距离为
的距离为![]() .
.
(2)延长![]() 交
交![]() 于点
于点![]() ,因为
,因为![]()
点![]() 到平面
到平面![]() 的距离为点
的距离为点![]() 到平面
到平面![]() 距离的
距离的![]() ,
,
![]() 点
点![]() 平面
平面![]() 的距离为
的距离为![]() ,而
,而![]() ,
,
直线![]() 与平面
与平面![]() 新角的正弦值为
新角的正弦值为![]() .
.
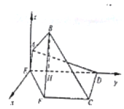
法二:(2)如图,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() 平面
平面![]() ,分别以
,分别以![]() 、
、![]() 、
、![]() 为
为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,设点
轴建立空间直角坐标系,设点![]() ,由于
,由于![]() ,
,
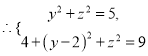 解得
解得![]() 于是
于是![]() ,所以线段
,所以线段![]() 的长度为
的长度为![]() .
.
即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
(3)从而![]() ,故
,故![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ,
,
则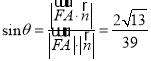
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程cos2x-sinx+a=0在(0,
 ]上有解,求a的取值范围.
]上有解,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=x2+ax+b(a,b∈R)的定义域为[-1,1],且|f(x)|的最大值为M.
(1)证明:|1+b|≤M;
(2)证明:M≥
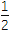 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x-3|-|x+1|,x∈R.
(1)解不等式f(x)<-1;
(2)设函数g(x)=|x+a|-4,且g(x)≤f(x)在x∈[-2,2]上恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在中学生测评中,分“优秀、合格、尚待改进”三个等级进行学生互评,某校高一年级有男生
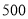 人,女生
人,女生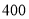 人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了
人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了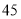 名学生的测评结果,并作出频数统计表如下:
名学生的测评结果,并作出频数统计表如下:等级
优秀
合格
尚待改进
频数
15
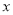
5
表一:男生
等级
优秀
合格
尚待改进
频数
15
3
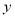
表二:女生
(1)从表二的非优秀学生中随机选取
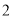 人交谈,求所选
人交谈,求所选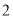 人中恰有
人中恰有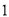 人测评等级为合格的概率;
人测评等级为合格的概率;(2)由表中统计数据填写
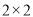 列联表,试采用独立性检验进行分析,能否在犯错误的概率不超过
列联表,试采用独立性检验进行分析,能否在犯错误的概率不超过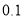 的前提下认为“测评结果优秀与性别有关”,参考数据与公示:
的前提下认为“测评结果优秀与性别有关”,参考数据与公示:  ,其中
,其中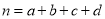
临界值表:
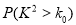
0.10
0.05
0.01
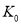
2.70
3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.
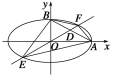
(1)若
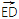 =6
=6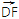 ,求k的值;
,求k的值;(2)求四边形AEBF面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
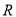 的函数
的函数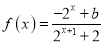 是奇函数.
是奇函数.(1)求
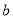 的值;
的值;(2)判断函数
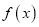 的单调性,并用定义证明;
的单调性,并用定义证明;(3)当
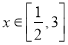 时,
时, 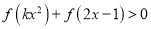 恒成立,求实数
恒成立,求实数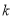 的取值范围.
的取值范围.
相关试题

