【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C: ![]() ,过点
,过点![]() 的直线l的参数方程为:
的直线l的参数方程为: 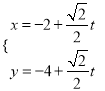 (t为参数),直线l与曲线C分别交于M、N两点.
(t为参数),直线l与曲线C分别交于M、N两点.
(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;
(Ⅱ)若| PM |,| MN |,| PN |成等比数列,求a的值.
参考答案:
【答案】(Ⅰ) ![]() (a > 0),
(a > 0), ![]() (Ⅱ)
(Ⅱ) ![]() .
.
【解析】试题分析:(1)利用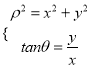 把极坐标方程转化为直角方程.把直线
把极坐标方程转化为直角方程.把直线![]() 中的参数消去即可得到其普通方程.(2)由直线方程中参数
中的参数消去即可得到其普通方程.(2)由直线方程中参数![]() 的几何意义可以得到
的几何意义可以得到![]() ,把直线的参数方程代入抛物线的普通方程得到
,把直线的参数方程代入抛物线的普通方程得到![]() 满足的方程,利用韦达定理把
满足的方程,利用韦达定理把![]() 转化为关于
转化为关于![]() 的方程,求出
的方程,求出![]() 即可.
即可.
解析:(Ⅰ)解:由 ![]() 得:
得: ![]() ,∴曲线
,∴曲线![]() 的直角坐标方程为:
的直角坐标方程为: ![]() ,由
,由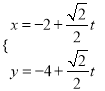 消去参数
消去参数![]() 得直线
得直线![]() 的普通方程为
的普通方程为![]() .
.
(Ⅱ)解:将直线l的参数方程 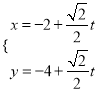 代入
代入![]() 中得:
中得: ![]() ,设
,设![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,则有
,则有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,即
,即 ![]() ,解得
,解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
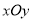 中,以
中,以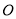 为极点,
为极点, 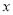 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线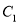 的方程是
的方程是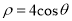 ,将
,将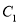 向上平移2个单位得到曲线
向上平移2个单位得到曲线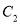 .
. (1)求曲线
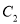 的极坐标方程;
的极坐标方程;(2)直线
 的参数方程为
的参数方程为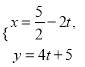 (
(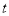 为参数),判断直线
为参数),判断直线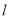 与曲线
与曲线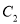 的位置关系.
的位置关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为2的圆内有两条圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度
 的图像大致为( )
的图像大致为( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
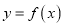 对定义域D内的每一个x1,都存在唯一的x2∈D,使得
对定义域D内的每一个x1,都存在唯一的x2∈D,使得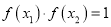 成立,则称f (x)为“自倒函数”.给出下列命题:
成立,则称f (x)为“自倒函数”.给出下列命题:①
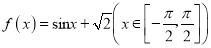 是自倒函数;
是自倒函数;②自倒函数f (x)可以是奇函数;
③自倒函数f (x)的值域可以是R;
④若
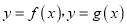 都是自倒函数,且定义域相同,则
都是自倒函数,且定义域相同,则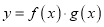 也是自倒函数.
也是自倒函数.则以上命题正确的是_______(写出所有正确命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
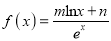 (m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是
(m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是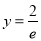 .
.(Ⅰ)求m、n的值;
(Ⅱ)求f (x)的最大值;
(Ⅲ)设
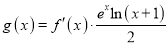 (其中
(其中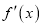 为f (x)的导函数),证明:对任意x > 0,都有
为f (x)的导函数),证明:对任意x > 0,都有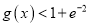 .
.(注:
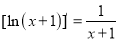 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】动点P到定点F(0,1)的距离比它到直线
 的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.(Ⅰ)求曲线C的方程;
(Ⅱ)求证:
 ;
;(Ⅲ)求△ABM的面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,
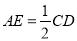 ,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.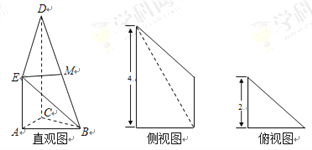
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
相关试题

