【题目】如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点, ![]() ,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
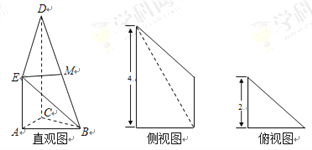
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求出该几何体的体积.
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)4.
【解析】试题分析:(1)去![]() 中点
中点![]() ,可以证明四边形
,可以证明四边形![]() 为平行四边形,从而得到
为平行四边形,从而得到![]() ,利用线面平行的判定定理可以得到
,利用线面平行的判定定理可以得到![]() 平面
平面![]() .(2)该几何体是一个四棱锥,其高为
.(2)该几何体是一个四棱锥,其高为![]() ,底面为直角梯形,上下底分别为
,底面为直角梯形,上下底分别为![]() ,高为
,高为![]() ,从而可以计算四棱锥的体积为
,从而可以计算四棱锥的体积为![]() .
.
解析: ![]() 为
为 ![]() 的中点,取
的中点,取 ![]() 中点
中点![]() ,连接
,连接![]() 则
则![]() , 且
, 且![]() ,
, ![]() 且
且 ![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形, ![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
(Ⅱ)解:由己知, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,又
,又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 是四棱锥
是四棱锥![]() 的高,梯形
的高,梯形![]() 的面积
的面积 ![]() ,
, ![]() ,即所求几何体的体积为4.
,即所求几何体的体积为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:
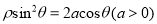 ,过点
,过点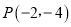 的直线l的参数方程为:
的直线l的参数方程为: 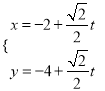 (t为参数),直线l与曲线C分别交于M、N两点.
(t为参数),直线l与曲线C分别交于M、N两点.(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;
(Ⅱ)若| PM |,| MN |,| PN |成等比数列,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
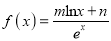 (m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是
(m、n为常数,e = 2.718 28…是自然对数的底数),曲线y = f (x)在点(1,f (1))处的切线方程是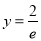 .
.(Ⅰ)求m、n的值;
(Ⅱ)求f (x)的最大值;
(Ⅲ)设
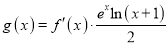 (其中
(其中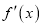 为f (x)的导函数),证明:对任意x > 0,都有
为f (x)的导函数),证明:对任意x > 0,都有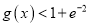 .
.(注:
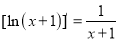 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】动点P到定点F(0,1)的距离比它到直线
 的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.
的距离小1,设动点P的轨迹为曲线C,过点F的直线交曲线C于A、B两个不同的点,过点A、B分别作曲线C的切线,且二者相交于点M.(Ⅰ)求曲线C的方程;
(Ⅱ)求证:
 ;
;(Ⅲ)求△ABM的面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把日均收看体育节目的时间超过50分钟的观众称为“超级体育迷”,已知5名“超级体育迷”中有2名女性,若从中任选2名,则至少有1名女性的概率为( )
A.
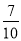 B.
B. 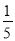
C.
 D.
D. 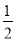
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过随机询问110名大学生是否爱好某项运动,得到列联表:
男
女
总计
爱好
40
20
60
不爱好
20
30
50
总计
60
50
110
由K2=
 ,得K2=
,得K2= ≈7.8.
≈7.8.附表:
P(K2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
参照附表,得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别有关”
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·辽宁五校联考)某车间加工零件的数量x与加工时间y的统计数据如表:
零件数x(个)
10
20
30
加工时间y(分钟)
21
30
39
现已求得上表数据的线性回归方程
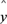 =
=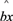 +
+ 中的
中的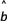 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )A. 84分钟 B. 94分钟
C. 102分钟 D. 112分钟
相关试题

