【题目】经过原点的直线与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆上不同于
为椭圆上不同于![]() 的一点,直线
的一点,直线![]() 的斜率均存在,且直线
的斜率均存在,且直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设![]() 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为![]() 的直线
的直线![]() 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于![]() 两点.若点
两点.若点![]() 在以
在以![]() 为直径的圆内部,求
为直径的圆内部,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析: (1)先利用点差法由直线![]() 的斜率之积为
的斜率之积为![]() 得
得![]() 之间关系,再解出离心率,(2)点
之间关系,再解出离心率,(2)点![]() 在以
在以![]() 为直径的圆内部,等价于
为直径的圆内部,等价于![]() ,而
,而![]() 可转化为
可转化为![]() 两点横坐标和与积的关系. 将直线
两点横坐标和与积的关系. 将直线![]() 方程与椭圆方程联立方程组,消去
方程与椭圆方程联立方程组,消去![]() 得关于
得关于![]() 的一元二次方程,利用韦达定理得
的一元二次方程,利用韦达定理得![]() 两点横坐标和与积关于
两点横坐标和与积关于![]() 的关系式,代入
的关系式,代入![]() ,解不等式可得
,解不等式可得![]() 的取值范围.
的取值范围.
试题解析:
(1)设![]() 则
则![]() ,∵点
,∵点![]() 三点均在椭圆上,
三点均在椭圆上,
∴![]() ,
, ![]() ,
,
∴ 作差得![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,记
,记![]() ,
,
∵![]() ,∴
,∴![]() ,
,
联立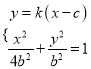 得
得![]() ,
, ![]() ,
,
∴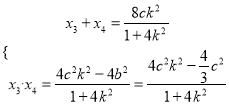 ,
,
当点![]() 在以
在以![]() 为直径的圆内部时,
为直径的圆内部时, ![]() ,
,
∴![]() ,
,
得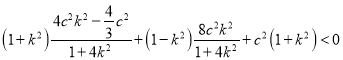 ,
,
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知曲线
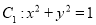 ,将曲线
,将曲线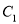 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的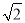 倍和
倍和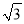 倍后,得到曲线
倍后,得到曲线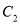
(1)试写出曲线
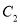 的参数方程;
的参数方程;(2)在曲线
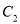 上求点
上求点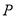 ,使得点
,使得点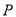 到直线
到直线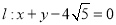 的距离最大,并求距离最大值.
的距离最大,并求距离最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
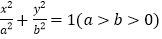 经过点
经过点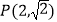 ,离心率
,离心率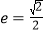 ,直线
,直线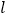 的方程为
的方程为 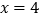 .
.(1)求椭圆
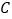 的方程;
的方程; (2)经过椭圆右焦点
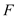 的任一直线(不经过点
的任一直线(不经过点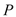 )与椭圆交于两点
)与椭圆交于两点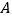 ,
,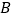 ,设直线
,设直线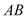 与
与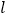 相交于点
相交于点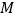 ,记
,记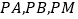 的斜率分别为
的斜率分别为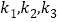 ,问:
,问: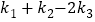 是否为定值,若是,求出此定值,若不是,请说明理由.
是否为定值,若是,求出此定值,若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
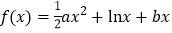 ,其中
,其中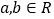 .
.(1)当
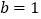 时,
时,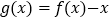 在
在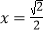 处取得极值,求函数
处取得极值,求函数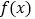 的单调区间;
的单调区间;(2)若
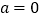 时,函数
时,函数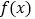 有两个不同的零点
有两个不同的零点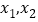 ,
,①求
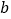 的取值范围;
的取值范围;②求证:
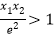 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校数学系2016年高等代数试题有6个题库,其中3个是新题库(即没有用过的题库),3个是旧题库(即至少用过一次的题库),每次期末考试任意选择2个题库里的试题考试.
(1)设2016年期末考试时选到的新题库个数为
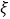 ,求
,求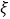 的分布列和数学期望;
的分布列和数学期望;(2)已知2016年时用过的题库都当作旧题库,求2017年期末考试时恰好到1个新题库的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A是由a-2,2a2+5a,12三个元素构成的,且-3∈A,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设某单位用2160万元购得一块空地,计划在该空地上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=购地总费用/建筑总面积)
相关试题

