【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,
时,![]() 在
在![]() 处取得极值,求函数
处取得极值,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 时,函数
时,函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,
①求![]() 的取值范围;
的取值范围;
②求证:![]() .
.
参考答案:
【答案】(Ⅰ)减区间为![]() ,增区间为
,增区间为![]() .(Ⅱ)①
.(Ⅱ)①![]() ②详见解析
②详见解析
【解析】试题分析:(Ⅰ)由极值定义可得![]() ,从而可解得
,从而可解得![]() .再根据导函数零点讨论导函数符号,结合导函数符号可得函数单调区间,(Ⅱ)①先利用导数分析函数单调性,即函数为非单调函数,导函数必有零点,再根据函数单调变化规律得函数最大值必大于零,又端点函数值趋于负无穷,根据零点存在定理可得函数必有两个零点,最后解最大值大于零时
.再根据导函数零点讨论导函数符号,结合导函数符号可得函数单调区间,(Ⅱ)①先利用导数分析函数单调性,即函数为非单调函数,导函数必有零点,再根据函数单调变化规律得函数最大值必大于零,又端点函数值趋于负无穷,根据零点存在定理可得函数必有两个零点,最后解最大值大于零时![]() 的取值范围,②
的取值范围,②![]() 等价于
等价于![]() ,由零点条件得
,由零点条件得![]() ,
,![]() ,两式相加与相减再相除消去
,两式相加与相减再相除消去![]() 得
得![]() ,因此转化为证明
,因此转化为证明![]() ,即需证明
,即需证明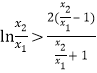 ,令
,令![]() ,构造函数
,构造函数![]() ,再利用导数研究函数单调性,得
,再利用导数研究函数单调性,得![]() ,即可得到结论.
,即可得到结论.
试题解析:(Ⅰ)解:由已知得![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以![]() .
.
则![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() ./span>
./span>
所以![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() .
.
(Ⅱ)①解:由已知![]() .
.
所以![]() ,
,
当![]() 时,显然
时,显然![]() 恒成立,此时函数
恒成立,此时函数![]() 在定义域内递增,
在定义域内递增,![]() 至多有一个零点,不合题意.当
至多有一个零点,不合题意.当![]() 时,令
时,令![]() 得
得![]() ,
,
令![]() 得
得![]() ;
;
令![]() 得
得![]() .
.
所以![]() 极大值为
极大值为![]() ,解得
,解得![]() .
.
且![]() 时,
时,![]() ,
,![]() 时,
时,![]() .
.
所以当![]() 时,
时,![]() 有两个零点.
有两个零点.
②证明:![]() ,
,![]() 为函数
为函数![]() 的两个零点,不妨设
的两个零点,不妨设![]() .
.
所以![]() ,
,![]() ,
,
两式相减得![]() ,两式相加得
,两式相加得![]() .
.
要证![]() ,即证
,即证![]() ,
,
即证![]() ,即证
,即证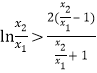 .
.
令![]() ,即证
,即证![]() .
.
令![]() ,则
,则![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·重庆高二检测)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
 AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC.
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知曲线
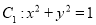 ,将曲线
,将曲线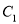 上所有点横坐标,纵坐标分别伸长为原来的
上所有点横坐标,纵坐标分别伸长为原来的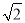 倍和
倍和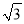 倍后,得到曲线
倍后,得到曲线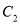
(1)试写出曲线
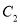 的参数方程;
的参数方程;(2)在曲线
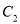 上求点
上求点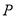 ,使得点
,使得点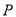 到直线
到直线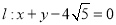 的距离最大,并求距离最大值.
的距离最大,并求距离最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
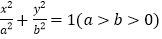 经过点
经过点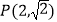 ,离心率
,离心率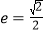 ,直线
,直线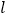 的方程为
的方程为 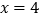 .
.(1)求椭圆
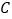 的方程;
的方程; (2)经过椭圆右焦点
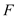 的任一直线(不经过点
的任一直线(不经过点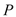 )与椭圆交于两点
)与椭圆交于两点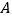 ,
,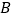 ,设直线
,设直线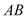 与
与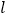 相交于点
相交于点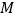 ,记
,记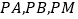 的斜率分别为
的斜率分别为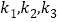 ,问:
,问: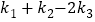 是否为定值,若是,求出此定值,若不是,请说明理由.
是否为定值,若是,求出此定值,若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过原点的直线与椭圆
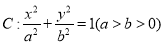 交于
交于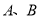 两点,点
两点,点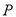 为椭圆上不同于
为椭圆上不同于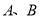 的一点,直线
的一点,直线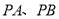 的斜率均存在,且直线
的斜率均存在,且直线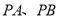 的斜率之积为
的斜率之积为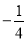 .
.(1)求椭圆
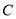 的离心率;
的离心率;(2)设
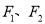 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为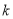 的直线
的直线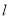 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于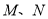 两点.若点
两点.若点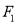 在以
在以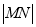 为直径的圆内部,求
为直径的圆内部,求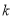 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校数学系2016年高等代数试题有6个题库,其中3个是新题库(即没有用过的题库),3个是旧题库(即至少用过一次的题库),每次期末考试任意选择2个题库里的试题考试.
(1)设2016年期末考试时选到的新题库个数为
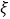 ,求
,求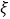 的分布列和数学期望;
的分布列和数学期望;(2)已知2016年时用过的题库都当作旧题库,求2017年期末考试时恰好到1个新题库的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A是由a-2,2a2+5a,12三个元素构成的,且-3∈A,求实数a的值.
相关试题

