【题目】某高校数学系2016年高等代数试题有6个题库，其中3个是新题库（即没有用过的题库），3个是旧题库（即至少用过一次的题库），每次期末考试任意选择2个题库里的试题考试.
（1）设2016年期末考试时选到的新题库个数为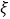
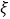，求的分布列和数学期望；
（2）已知2016年时用过的题库都当作旧题库，求2017年期末考试时恰好到1个新题库的概率．
【答案】（Ⅰ）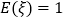
，分布列见解析（Ⅱ）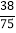
【解析】试题分析：（Ⅰ）先确定随机变量所有可能取值,再分别求对应概率,列表可得分布列,最后根据数学期望公式求期望,（Ⅱ）按2016年时用过的题库分类讨论: 2016年期末考试时取到0个新题库时,2017年期末考试时恰好到1个新题库的概率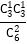
; 2016年期末考试时取到1个新题库时,2017年期末考试时恰好到1个新题库的概率
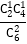; 2016年期末考试时取到2个新题库时,2017年期末考试时恰好到1个新题库的概率
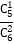;再根据2016年期末考试时取到
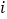个新题库对应概率可得所求概率为
.
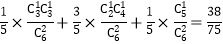试题解析：（Ⅰ）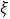
的所有可能取值为0，1，2，
设“2016年期末考试时取到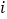个新题库（即
）”为事件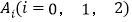
．
又因为6个题库中，其中3个是新题库，3个是旧题库，
所以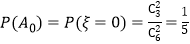
；
；
，
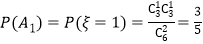所以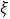的分布列为
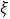
| 0 | 1 | 2 |
P |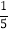 
| 
|
|
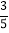
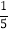
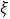的数学期望为
．
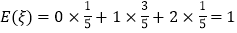（Ⅱ）设“从6个题库中任意取出2个题库，恰好取到一个新题库”为事件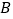
，
则“2017年时恰好取到一个新题库”就是事件
，而事件
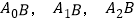互斥，
所以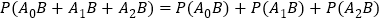
．
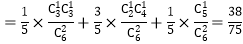所以2017年时恰好取到一个新题库的概率为．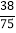
相关试题
-
科目：
来源：
题型：
查看答案和解析>>
-
科目：
来源：
题型：
查看答案和解析>>
-
科目：
来源：
题型：
查看答案和解析>>
-
科目：
来源：
题型：
【题目】已知集合A是由a－2,2a2＋5a,12三个元素构成的，且－3∈A，求实数a的值.
-
科目：
来源：
题型：
【题目】设某单位用2160万元购得一块空地，计划在该空地上建造一栋至少10层，每层2000平方米的楼房．经测算，如果将楼房建为x（x≥10）层，则每平方米的平均建筑费用为560＋48x（单位：元）．
（1）写出楼房平均综合费用y关于建造层数x的函数关系式；
（2）该楼房应建造多少层时，可使楼房每平方米的平均综合费用最少？最少值是多少？
（注：平均综合费用＝平均建筑费用＋平均购地费用，平均购地费用＝购地总费用/建筑总面积）
-
科目：
来源：
题型：
【题目】下列5个命题中正确命题的个数是( )
①对于命题p：x∈R，使得x2＋x＋1<0，则綈p：x∈R，均有x2＋x＋1>0；
②m＝3是直线(m＋3)x＋my－2＝0与直线mx－6y＋5＝0互相垂直的充要条件；
③已知回归直线的斜率的估计值为1.23，样本点的中心为(4,5)，则线性回归方程为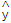
＝1.23x＋0.08；
④若实数x，y∈[－1,1]，则满足x2＋y2≥1的概率为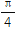
；
⑤曲线y＝x2与y＝x所围成图形的面积是S＝ (x－x2)dx.
A．2 B．3 C．4 D．5
关闭
搜索
