【题目】三棱锥P﹣ABC中,PO⊥面ABC,垂足为O,若PA⊥BC,PC⊥AB,求证: 
(1)AO⊥BC
(2)PB⊥AC.
参考答案:
【答案】
(1)证明:∵PO⊥平面ABC,
又BC平面ABC,
∴PO⊥BC
又PA⊥BC,PO∩PA=P,
∴BC⊥平面PAO
∵AO平面PAO
∴AO⊥BC
(2)证明:PO⊥面ABC,垂足为O,PA⊥BC,PC⊥AB,则OA⊥BC,OC⊥AB,又三角形的高交于一点,∴BO⊥AC,∴PB⊥AC
【解析】(1)要证AO⊥BC,只需要证BC⊥平面PAO,要只需要证PO⊥BC,PA⊥BC,只需要证PA⊥平面PBC,根据已知条件可证;(2)利用三垂线定理以及三角形的高 交于一点得证.
【考点精析】通过灵活运用直线与平面垂直的性质,掌握垂直于同一个平面的两条直线平行即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=1﹣
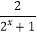 .
.
(1)求证:f(x)是定义域内的增函数;
(2)当x∈[0,1]时,求f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是奇函数,且定义域为(﹣∞,0)∪(0,+∞).若x<0时,f(x)=﹣x﹣1.
(1)求f(x)的解析式;
(2)解关于x的不等式f(x)>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆C:
 的离心率e=
的离心率e= 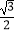 ,左顶点M到直线
,左顶点M到直线  =1的距离d=
=1的距离d= 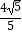 ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设直线l与椭圆C相交于A,B两点,若以AB为直径的圆经过坐标原点,证明:点O到直线AB的距离为定值;
(3)在(2)的条件下,试求△AOB的面积S的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=(log2x)2﹣2alog2x+b(x>0).当x=
 时,f(x)有最小值﹣1.
时,f(x)有最小值﹣1.
(1)求a与b的值;
(2)求满足f(x)<0的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是BC的中点.
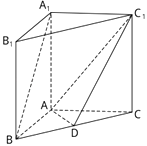
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD﹣A1B1C1的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(x+1)﹣f(x)=4x+1,且f(0)=3.
(1)求f(x)的解析式;
(2)设g(x)=f(2x),求g(x)在[﹣3,0]的最大值与最小值.
相关试题

