【题目】已知f(x)是R上的奇函数,且当x∈[0,+∞)时, ![]() . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)运用函数单调性定义证明f(x)在定义域R上是增函数.
参考答案:
【答案】解:(Ⅰ)设x∈(﹣∞,0), 则﹣x∈(0,+∞),
∵当x∈[0,+∞)时,f(x)= ![]()
∴f(﹣x)= ![]() ,
,
∵f(x)是R上的奇函数,
∴f(﹣x)=﹣f(x),
即f(﹣x)= ![]() =﹣f(x),
=﹣f(x),
∴f(x)=﹣ ![]() ,x∈(﹣∞,0),
,x∈(﹣∞,0),
∴f(x)= 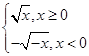 .
.
(Ⅱ)∵f(x)是R上的奇函数,
∴只需要证明函数f(x)在[0,+∞)上单调递增即可,
设x2>x1≥0,
则 ![]() ,
,
∵x2>x1≥0,
∴x2﹣x1>0, ![]() ,
,
即 ![]() >0,
>0,
∴f(x2)>f(x1),即函数在[0,+∞)上单调递增,
∴f(x)在定义域R上是增函数
【解析】(Ⅰ)根据函数奇偶性的性质即可求f(x)的解析式;(Ⅱ)根据函数单调性定义证明f(x)在定义域R上是增函数.
【考点精析】通过灵活运用函数单调性的判断方法和函数奇偶性的性质,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 是直线
是直线 与函数
与函数 图像的两个相邻的交点,且
图像的两个相邻的交点,且 .
.(1)求
 的值和函数
的值和函数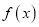 的单调增区间;
的单调增区间; (2)将函数
 的图象上各点的横坐标伸长为原来的
的图象上各点的横坐标伸长为原来的 倍(纵坐标不变),再将得到的图象向左平移
倍(纵坐标不变),再将得到的图象向左平移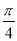 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 的对称轴方程.
的对称轴方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a为实数,函数f(x)=2x2+(x﹣a)|x﹣a|.
(1)若f(0)≥1,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】若Ai(i=1,2,3,…,n)是△AOB所在平面内的点,且
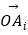
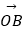 =
= 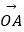
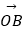 ,给出下列说法:
,给出下列说法:
·(1)|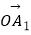 |=|
|=| 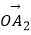 |=|
|=| 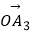 |=…=|
|=…=| 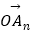 |
|
·(2)|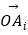 |的最小值一定是|
|的最小值一定是| 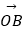 |
|
·(3)点A和点Ai一定共线
·(4)向量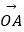 及
及 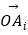 在向量
在向量 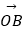 方向上的投影必定相等
方向上的投影必定相等
其中正确的个数是( )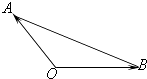
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(1+x),g(x)=loga(1+kx),其中a>0且a≠1. (Ⅰ)当k=﹣2时,求函数h(x)=f(x)+g(x)的定义域;
(Ⅱ)若函数H(x)=f(x)﹣g(x)是奇函数(不为常函数),求实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sinx+1. (Ⅰ)设ω为大于0的常数,若f(ωx)在区间
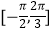 上单调递增,求实数ω的取值范围;
上单调递增,求实数ω的取值范围;
(Ⅱ)设集合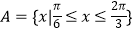 ,B={x||f(x)﹣m|<2},若A∪B=B,求实数m的取值范围.
,B={x||f(x)﹣m|<2},若A∪B=B,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意的x1∈[﹣1,2],存在x0∈[﹣1,2],使g(x1)=f(x0),则a的取值范围是( )
A.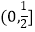
B.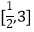
C.[3,+∞)
D.(0,3]
相关试题

